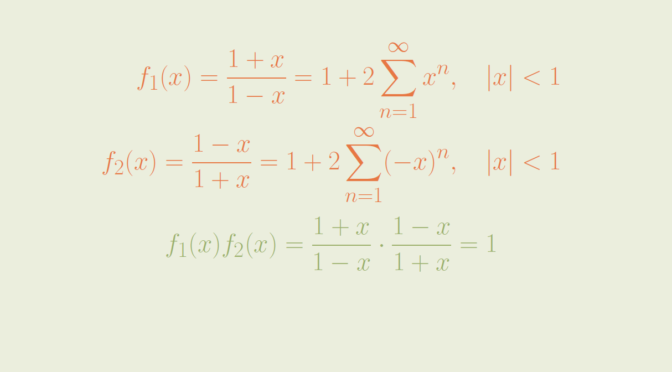We look here at the radius of convergence of the sum and product of power series.

Let’s recall that for a power series \(\displaystyle \sum_{n=0}^\infty a_n x^n\) where \(0\) is not the only convergence point, the radius of convergence is the unique real \(0 < R \le \infty\) such that the series converges whenever \(\vert x \vert < R\) and diverges whenever \(\vert x \vert > R\).

Given two power series with radii of convergence \(R_1\) and \(R_2\), i.e.
\begin{align*}
\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n, \ \vert x \vert < R_1 \\ \displaystyle f_2(x) = \sum_{n=0}^\infty b_n x^n, \ \vert x \vert < R_2 \end{align*} The sum of the power series \begin{align*} \displaystyle f_1(x) + f_2(x) &= \sum_{n=0}^\infty a_n x^n + \sum_{n=0}^\infty b_n x^n \\ &=\sum_{n=0}^\infty (a_n + b_n) x^n \end{align*} and its Cauchy product:
\begin{align*}
\displaystyle f_1(x) \cdot f_2(x) &= \left(\sum_{n=0}^\infty a_n x^n\right) \cdot \left(\sum_{n=0}^\infty b_n x^n \right) \\
&=\sum_{n=0}^\infty \left( \sum_{l=0}^n a_l b_{n-l}\right) x^n
\end{align*}
both have radii of convergence greater than or equal to \(\min \{R_1,R_2\}\).

The radii can indeed be greater than \(\min \{R_1,R_2\}\). Let’s give examples.

Sum of power series

Consider any power series \(\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n\) having a non-zero finite radius of convergence \(R_1\). Then the radius of convergence of the power series \(\displaystyle f_2(x) = -f_1(x) = \sum_{n=0}^\infty -a_n x^n\) is also equal to \(R_1\). The sum \(f_1(x) + f_2(x)\) is the always vanishing power series whose radius of convergence is infinite, hence greater than \(R_1\).

Product of power series

Here we take
\begin{align*}
\displaystyle f_1(x) &=\frac{1+x}{1-x} = (1+x) \left(\sum_{n=0}^\infty x^n\right)\\
&= \sum_{n=0}^\infty x^n + x \sum_{n=0}^\infty x^n\\
&=1 + 2 \sum_{n=1}^\infty x^n, \qquad \vert x \vert < 1 \end{align*} with radius of convergence \(R_1=1\). And \(f_2(x)=f_1(-x)=\frac{1-x}{1+x}\). We have \[\displaystyle f_2(x)= 1 + 2 \sum_{n=1}^\infty (-x)^n\] The radius of convergence of \(f_2(x)\) is also equal to \(1\). The product power series is \[f_1(x) f_2(x) = \frac{1+x}{1-x} \cdot \frac{1-x}{1+x}=1\] and has an infinite radius of convergence. For that matter, one can directly verify that the Cauchy product of \(f_1(x)\) and \(f_2(x)\) has all coefficients vanishing except the first one which is equal to \(1\).