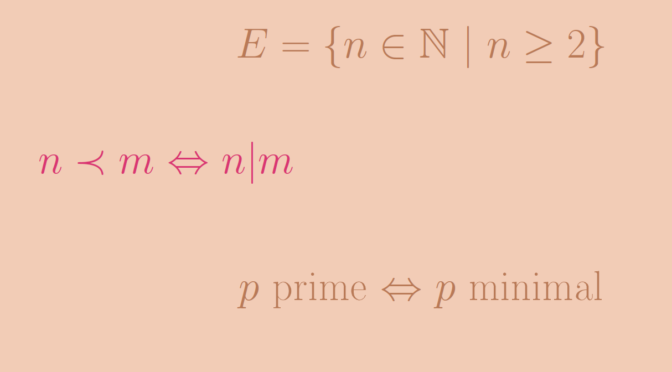Let’s consider a partially ordered set (or poset) \(E\).

If \(E\) is totally ordered, \(E\) has at most one minimal element. If \(E\) is not totally ordered, \(E\) can have multiple minimal elements. We provide an example for the set \(E=\{n \in \mathbb N \ | \ n \ge 2\}\). For two natural numbers \(n\) and \(m\), we write \(n|m\) if \(n\) divides \(m\). One easily sees that this yields a partial order.

The minimal elements of \(E\) are the elements not having divisors, this is the case for all prime numbers \(p \in E\).

\(E\) has an infinite number of minimal elements which are the prime numbers.