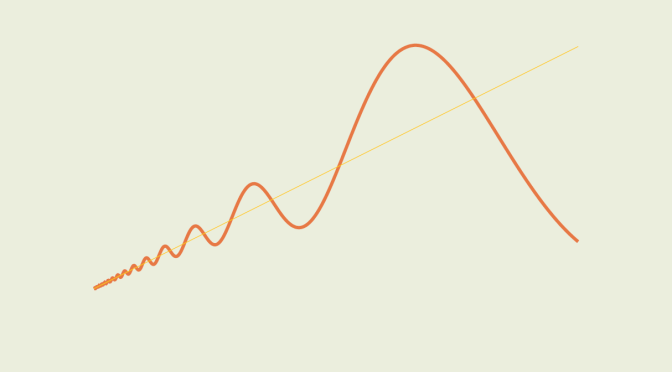
From the mean value theorem, a real function whose derivative is strictly positive at every point of an interval is strictly increasing. In particular, a continuously differentiable function \(f\) defined in a non-degenerate interval \(I\) with a strictly positive derivative at a point \(a\) of the interval is strictly increasing near that point. For the proof, we just have to notice that as \(f^\prime\) is continuous and \(f^\prime(a) > 0\), \(f^\prime\) is strictly positive within an interval \(J \subset I\) containing \(a\). By the mean value theorem, \(f\) is strictly increasing on \(J\).

We now suppose that \(f\) is differentiable on an interval \(I\) containing \(0\) with \(f^\prime(0)>0\). For \(x>0\) sufficiently close to zero we have \(\displaystyle \frac{f(x)-f(0)}{x-0} > \frac{f^\prime(0)}{2}>0\), hence \(f(x)>f(0)\). But that doesn’t imply that \(f\) is strictly increasing in a neighborhood of zero. Let’s prove it with a counterexample.

Consider the function:
\[\begin{array}{l|rcl}
f : & \mathbb{R} & \longrightarrow & \mathbb{R} \\
& 0 & \longmapsto & 0 \\
& x & \longmapsto & x + 4x^2 \sin(\frac{1}{x}) \text{ for } x \neq 0 \end{array}\] \(f\) is continuous and differentiable at all non-zero points. \(f\) is continuous at \(0\) as for \(x \in \mathbb{R}\) we have \(\vert f(x) – f(0) \vert = \vert f(x) \vert \le \vert x \vert + 4 \vert x \vert^2\). The function \(g: x \mapsto x^2 \sin(\frac{1}{x})\) is differentiable at \(0\) as for \(x \neq 0\) we have the inequality:
\[\left\vert \frac{g(x)-g(0)}{x-0} \right\vert=\left\vert \frac{g(x)}{x}\right\vert \le \vert x \vert\] proving that \(g\) is differentiable at \(0\) with a derivative equal to zero at that point. As \(f(x)=4g(x)+x\), \(f\) is differentiable at \(0\) with \(f^\prime(0)=1\). For all \(x \neq 0\) we have:
\[f^\prime(x)=1-4 \cos(\frac{1}{x})+8x \sin(\frac{1}{x})\] Therefore for \(\vert x \vert \le 1/8\) we get:
\[-1 \le f^\prime(x)-\left (1-4 \cos(\frac{1}{x}) \right ) \le 1\] and
\[-4 \cos(\frac{1}{x}) \le f^\prime(x)\le 2-4 \cos(\frac{1}{x})\] Consequently for \(n \ge 1\) integer:

• when \(\displaystyle \frac{1}{x} \in (2n\pi + \frac{2\pi}{3},2n\pi + \frac{4\pi}{3})\) we have \(\displaystyle \cos(\frac{1}{x}) \le -\frac{1}{2}\) hence for \(\displaystyle x \in (\frac{1}{2n\pi + \frac{4\pi}{3}},\frac{1}{2n\pi + \frac{2\pi}{3}})\): \(f^\prime(x) \ge -4 \cos(\frac{1}{x}) \ge 2\). Which implies that \(f\) is strictly increasing on each interval \((\frac{1}{2n\pi + \frac{4\pi}{3}},\frac{1}{2n\pi + \frac{2\pi}{3}})\).
• Similarly for \(\displaystyle \frac{1}{x} \in ((2n+1)\pi + \frac{5\pi}{6},(2n+1)\pi + \frac{7\pi}{6})\) we have \(\displaystyle \cos(\frac{1}{x}) \ge \frac{\sqrt{3}}{2}\) hence for \(\displaystyle x \in (\frac{1}{(2n+1)\pi + \frac{7\pi}{6}},\frac{1}{(2n+1)\pi + \frac{5\pi}{6}})\): \(f^\prime(x) \le 2-4 \cos(\frac{1}{x}) \le 2(1-\sqrt{3}) <0\). Which implies that \(f\) is strictly decreasing on each interval \((\frac{1}{(2n+1)\pi + \frac{7\pi}{6}},\frac{1}{(2n+1)\pi + \frac{5\pi}{6}})\).

Finally \(f\) is not strictly increasing in any neighborhood of \(0\) although \(f^\prime (0) >0\).