The purpose of this article is to provide some basic counterexamples on real series. Counterexamples are provided as answers to questions.
Unless otherwise stated, \((u_n)_{n \in \mathbb{N}}\) and \((v_n)_{n \in \mathbb{N}}\) are two real sequences.
If \((u_n)\) is non-increasing and converges to zero then \(\sum u_n\) converges?
Is not true. A famous counterexample is the harmonic series \(\sum \frac{1}{n}\) which doesn’t converge as \[
\displaystyle \sum_{k=p+1}^{2p} \frac{1}{k} \ge \sum_{k=p+1}^{2p} \frac{1}{2p} = 1/2,\] for all \(p \in \mathbb N\).
If \(u_n = o(1/n)\) then \(\sum u_n\) converges?
Does not hold as can be seen considering \(u_n=\frac{1}{n \ln n}\) for \(n \ge 2\). Indeed \(\int_2^x \frac{dt}{t \ln t} = \ln(\ln x) – \ln (\ln 2)\) and therefore \(\int_2^\infty \frac{dt}{t \ln t}\) diverges. We conclude that \(\sum \frac{1}{n \ln n}\) diverges using the integral test. However \(n u_n = \frac{1}{\ln n}\) converges to zero.
If \(u_n = o(v_n)\) and \(\sum v_n\) converges then \(\sum u_n\) converges?
Is not true as we can see taking \(v_n = \frac{(-1)^n}{n}\) and \(u_n=\frac{1}{n \ln n}\). \(\sum v_n\) converges according to the alternating series test and \(\sum u_n\) diverges according to previous paragraph. However \[
\lim\limits_{n \to \infty} \left\vert \frac{u_n}{v_n} \right\vert = \lim\limits_{n \to \infty} \frac{1}{\ln n} = 0.\]
If \(\sum u_n\) is a positive converging series then \(\frac{u_{n+1}}{u_n}\) is bounded?
Not either. Have a look at \[
u_n=\begin{cases} \frac{1}{n^2} & \text{for } n \text{ even} \\
\frac{1}{2^n} & \text{for } n \text{ odd.} \end{cases}\] Then for \(p \in \mathbb N\) \[
\frac{u_{2p+1}}{u_{2p}} = \frac{2^{2p+1}}{4p^2}\] diverges to \(\infty\). However \(\sum u_n\) converges as \(\sum \frac{1}{n^2}\) and \(\sum \frac{1}{2^n}\) both converge.

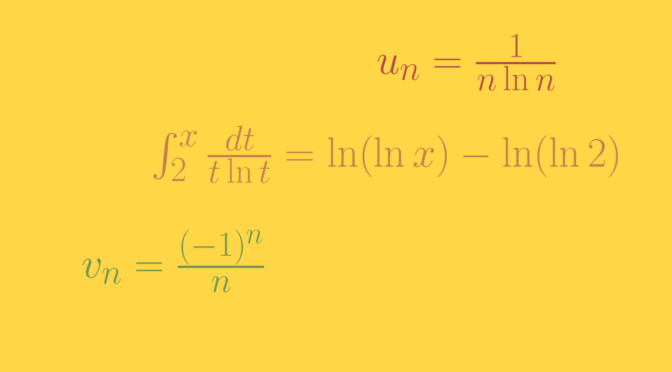
One thought on “Counterexamples around series (part 1)”