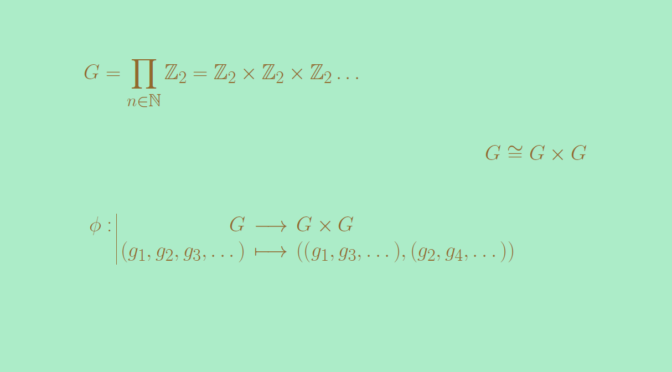Let’s provide an example of a nontrivial group \(G\) such that \(G \cong G \times G\). For a finite group \(G\) of order \(\vert G \vert =n > 1\), the order of \(G \times G\) is equal to \(n^2\). Hence we have to look at infinite groups in order to get the example we’re seeking for.

We take for \(G\) the infinite direct product \[
G = \prod_{n \in \mathbb N} \mathbb Z_2 = \mathbb Z_2 \times \mathbb Z_2 \times \mathbb Z_2 \dots,\] where \(\mathbb Z_2\) is endowed with the addition. Now let’s consider the map \[
\begin{array}{l|rcl}
\phi : & G & \longrightarrow & G \times G \\
& (g_1,g_2,g_3, \dots) & \longmapsto & ((g_1,g_3, \dots ),(g_2, g_4, \dots)) \end{array}\]

From the definition of the addition in \(G\) it follows that \(\phi\) is a group homomorphism. \(\phi\) is onto as for any element \(\overline{g}=((g_1, g_2, g_3, \dots),(g_1^\prime, g_2^\prime, g_3^\prime, \dots))\) in \(G \times G\), \(g = (g_1, g_1^\prime, g_2, g_2^\prime, \dots)\) is an inverse image of \(\overline{g}\) under \(\phi\). Also the identity element \(e=(\overline{0},\overline{0}, \dots)\) of \(G\) is the only element of the kernel of \(G\). Hence \(\phi\) is also one-to-one. Finally \(\phi\) is a group isomorphism between \(G\) and \(G \times G\).