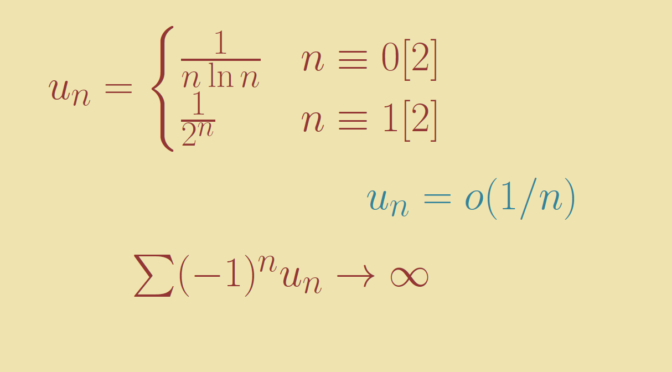We follow the article counterexamples around series (part 1) providing additional funny series examples.
If \(\sum u_n\) converges and \((u_n)\) is non-increasing then \(u_n = o(1/n)\)?
This is true. Let’s prove it.
The hypotheses imply that \((u_n)\) converges to zero. Therefore \(u_n \ge 0\) for all \(n \in \mathbb N\). As \(\sum u_n\) converges we have \[
\displaystyle \lim\limits_{n \to \infty} \sum_{k=n/2}^{n} u_k = 0.\] Hence for \(\epsilon \gt 0\), one can find \(N \in \mathbb N\) such that \[
\epsilon \ge \sum_{k=n/2}^{n} u_k \ge \frac{1}{2} (n u_n) \ge 0\] for all \(n \ge N\). Which concludes the proof.
\(\sum u_n\) convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) convergent?
Is not true as we can see taking \(u_n = \frac{(-1)^n}{n}\). \(\sum u_n\) converges according to the alternating series test. However for \(n \in \mathbb N\) \[
\sum_{k=1}^n u_{2k} = \sum_{k=1}^n \frac{1}{2k} = 1/2 \sum_{k=1}^n \frac{1}{k}.\] Hence \(\sum u_{2n}\) diverges as the harmonic series diverges.
\(\sum u_n\) absolutely convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) absolutely convergent?
This is true and the proof is left to the reader.
\(\sum u_n\) is a positive convergent series then \((\sqrt[n]{u_n})\) is bounded?
Is true. If not, there would be a subsequence \((u_{\phi(n)})\) such that \(\sqrt[\phi(n)]{u_{\phi(n)}} \ge 2\). Which means \(u_{\phi(n)} \ge 2^{\phi(n)}\) for all \(n \in \mathbb N\) and implies that the sequence \((u_n)\) is unbounded. In contradiction with the convergence of the series \(\sum u_n\).
If \((u_n)\) is strictly positive with \(u_n = o(1/n)\) then \(\sum (-1)^n u_n\) converges?
It does not hold as we can see with \[
u_n=\begin{cases} \frac{1}{n \ln n} & n \equiv 0 [2] \\
\frac{1}{2^n} & n \equiv 1 [2] \end{cases}\] Then for \(n \in \mathbb N\) \[
\sum_{k=1}^{2n} (-1)^k u_k \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – \sum_{k=1}^{2n} \frac{1}{2^k} \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – 1.\] As \(\sum \frac{1}{2k \ln 2k}\) diverges as can be proven using the integral test with the function \(x \mapsto \frac{1}{2x \ln 2x}\), \(\sum (-1)^n u_n\) also diverges.