Following the article on differentiability of multivariable real functions (part 1), we look here at second derivatives. We consider a function \(f : \mathbb R^n \to \mathbb R\) with \(n \ge 2\).

Schwarz’s theorem states that if \(f : \mathbb R^n \to \mathbb R\) has continuous second partial derivatives at any given point in \(\mathbb R^n\), then for \((a_1, \dots, a_n) \in \mathbb R^n\) and \(i,j \in \{1, \dots, n\}\):
\[\frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, \dots, a_n)=\frac{\partial^2 f}{\partial x_j \partial x_i}(a_1, \dots, a_n)\]

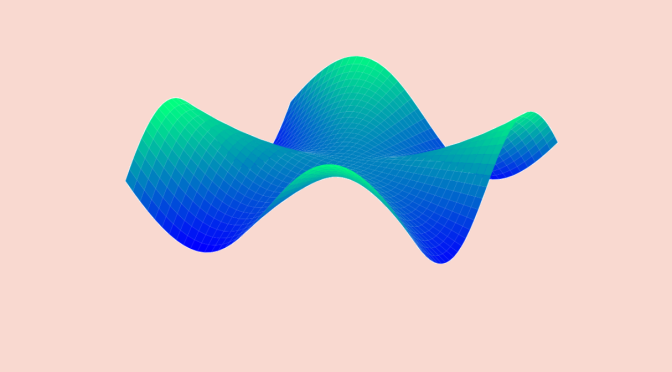
A function for which \(\frac{\partial^2 f}{\partial x \partial y}(0,0) \neq \frac{\partial^2 f}{\partial y \partial x}(0,0)\)

We consider:
\[\begin{array}{l|rcl}
f : & \mathbb R^2 & \longrightarrow & \mathbb R \\
& (0,0) & \longmapsto & 0\\
& (x,y) & \longmapsto & \frac{xy(x^2-y^2)}{x^2+y^2} \text{ for } (x,y) \neq (0,0)
\end{array}\]

\(f\) is defined and indefinitely differentiable at all points different from the origin. For \((x,y) \neq (0,0)\):
\begin{align*} \left\vert \frac{f(x,y)}{\sqrt{x^2+y^2}} \right\vert & = \left\vert \frac{xy(x^2-y^2)}{\sqrt{x^2+y^2}(x^2+y^2)} \right\vert\\
& \le \left\vert \frac{xy}{\sqrt{x^2+y^2}} \right\vert\\
& \le \frac{(\vert x \vert + \vert y \vert)^2}{2 \sqrt{x^2+y^2}}\\
& \le \sqrt{x^2+y^2}\end{align*} as we have for all \((x,y) \in \mathbb R^2\): \(\vert xy \vert \le \frac{(\vert x \vert +\vert y \vert)^2}{2}\) and \((\vert x \vert +\vert y \vert)^2 \le 2 (x^2+y^2)\). This proves that \(f\) is continuous and differentiable at the origin, with \(f(0,0)=0\) and a Fréchet derivative equal to zero at the origin. So \[\frac{\partial f}{\partial x}(0,0)=\frac{\partial f}{\partial y}(0,0)=0\] We now look at the mixed partial derivatives.

For \((x,y) \neq (0,0)\):\[\begin{cases}
\frac{\partial f}{\partial x}(x,y) = \frac{(x^2+y^2)(3x^2y-y^3)+2x^2y(y^2-x^2)}{(x^2+y^2)^2}\\
\frac{\partial f}{\partial y}(x,y) = \frac{(x^2+y^2)(x^3-3x y^2)+2xy^2(y^2-x^2)}{(x^2+y^2)^2}
\end{cases}\] In particular:
\begin{align*}
\frac{\partial f}{\partial x}(0,y) &= -y \text{ for } y \neq 0\\
\frac{\partial f}{\partial x}(x,0) &= x \text{ for } x \neq 0
\end{align*} which implies \[\frac{\partial^2 f}{\partial x \partial y}(0,0) =1 \neq -1 = \frac{\partial^2 f}{\partial y \partial x}(0,0)\]
The mixed second derivatives of \(f\) are not symmetric.