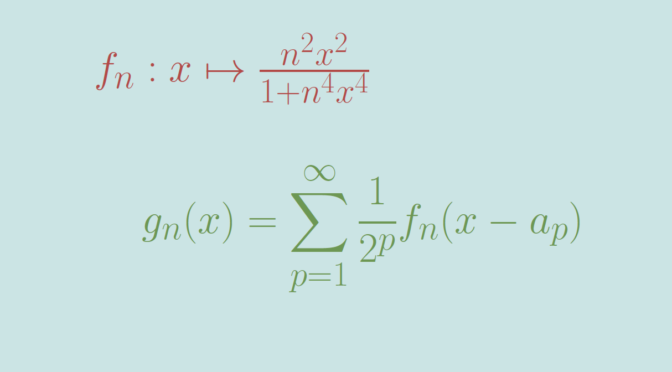We provide in this article an example of a pointwise convergent sequence of real functions that doesn’t converge uniformly on any interval.

Let’s consider a sequence \((a_p)_{p \in \mathbb N}\) enumerating the set \(\mathbb Q\) of rational numbers. Such a sequence exists as \(\mathbb Q\) is countable.

Now let \((g_n)_{n \in \mathbb N}\) be the sequence of real functions defined on \(\mathbb R\) by \[
g_n(x) = \sum_{p=1}^{\infty} \frac{1}{2^p} f_n(x-a_p)\] where \(f_n : x \mapsto \frac{n^2 x^2}{1+n^4 x^4}\) for \(n \in \mathbb N\).

\(f_n\) main properties

\(f_n\) is a rational function whose denominator doesn’t vanish. Hence \(f_n\) is indefinitely differentiable. As \(f_n\) is an even function, we can study it only on \([0,\infty)\).

We have \[
f_n^\prime(x)= 2n^2x \frac{1-n^4x^4}{(1+n^4 x^4)^2}.\] \(f_n^\prime\) vanishes at zero (like \(f_n\)) is positive on \((0,\frac{1}{n})\), vanishes at \(\frac{1}{n}\) and is negative on \((\frac{1}{n},\infty)\). Hence \(f_n\) has a maximum at \(\frac{1}{n}\) with \(f_n(\frac{1}{n}) = \frac{1}{2}\) and \(0 \le f_n(x) \le \frac{1}{2}\) for all \(x \in \mathbb R\).

Also for \(x \neq 0\) \[
0 \le f_n(x) =\frac{n^2 x^2}{1+n^4 x^4} \le \frac{n^2 x^2}{n^4 x^4} = \frac{1}{n^2 x^2}\] consequently \[
0 \le f_n(x) \le \frac{1}{n} \text{ for } x \ge \frac{1}{\sqrt{n}}.\]

\((g_n)\) converges pointwise to zero

First, one can notice that \(g_n\) is well defined. For \(x \in \mathbb R\) and \(p \in \mathbb N\) we have \(0 \le \frac{1}{2^p} f_n(x-a_p) \le \frac{1}{2^p} \cdot\ \frac{1}{2}=\frac{1}{2^{p+1}}\) according to previous paragraph. Therefore the series of functions \(\sum \frac{1}{2^p} f_n(x-a_p)\) is normally convergent. \(g_n\) is also continuous as for all \(p \in \mathbb N\) \(x \mapsto \frac{1}{2^p} f_n(x-a_p)\) is continuous.

Now fix \(x \in \mathbb R\). For \(0< \epsilon < \frac{1}{2}\) we denote \(p_\epsilon = \sup\{p \in \mathbb N \ ; \ \frac{1}{2^p} > \epsilon\}\) and \(A_\epsilon= \{a_p \ ; \ p \le p_\epsilon\}\). \(A_\epsilon\) is a finite subset of reals, hence the distance \(\delta = d(x,A_\epsilon \setminus \{x\})\) is strictly positive. Denoting \(N=\lceil \sup(\frac{1}{\epsilon},\frac{1}{\delta^2}) \rceil\), we have for \(n \ge N\)\[
\vert x – a_p \vert \ge \delta \ge \frac{1}{\sqrt{n}} \text{ for } a_p \in A_\epsilon \setminus \{x\}\] and therefore \(0 \le f_n(x-a_p) \le \frac{1}{n} \le \epsilon\) for \(a_p \in A_\epsilon\). Finally for \(n \ge N\)\[
\begin{aligned}
0 &\le g_n(x) = \sum_{p=1}^{\infty} \frac{1}{2^p} f_n(x-a_p)\\
&=\sum_{p=1}^{p_\epsilon} \frac{1}{2^p} f_n(x-a_p) + \sum_{p=p_\epsilon+1}^\infty \frac{1}{2^p} f_n(x-a_p)\\
&\le \sum_{p=1}^{p_\epsilon} \frac{1}{2^p} \epsilon + \sum_{p=p_\epsilon+1}^\infty \frac{1}{2^p} \frac{1}{2}\\
&\le \epsilon\sum_{p=1}^\infty \frac{1}{2^p} + \frac{1}{2}\sum_{p=p_\epsilon+1}^\infty \frac{1}{2^p}\\
&\le \epsilon\sum_{p=1}^\infty \frac{1}{2^p} + \frac{1}{2}\sum_{p=p_\epsilon+1}^\infty \frac{1}{2^p}\\
&= \epsilon + \frac{1}{2^{p_\epsilon+1}} \le 2 \epsilon.\\
\end{aligned}\] This concludes the proof that \((g_n)\) converges pointwise to zero. An alternate proof can be based on Lebesgue’s dominated convergence theorem using the discrete measure \(\displaystyle \sum_{p \in \mathbb N} \frac{1}{2^p} \delta_{a_p}\) where \(\delta_x\) denotes the Dirac measure centered on some fixed point \(x\).

\((g_n)\) doesn’t converge uniformly on any open interval

Consider an open interval \((u,v)\) with \(u < v\). As \(\mathbb Q\) is dense in \(\mathbb R\), it exists \(q \in \mathbb N\) such that \(a_q \in (u,v)\). As \((u,v)\) is open, we also have \(a_q + 1/n \in (u,v)\) for \(n\) large enough. Then \[ g_n(a_q+1/n) \ge \frac{1}{2^q} f_n(a_q+1/n-a_q)=\frac{1}{2^q}f_n(1/n)=\frac{1}{2^{q+1}}\] proving that \((g_n)\) doesn't converge uniformly on \((u,v)\).