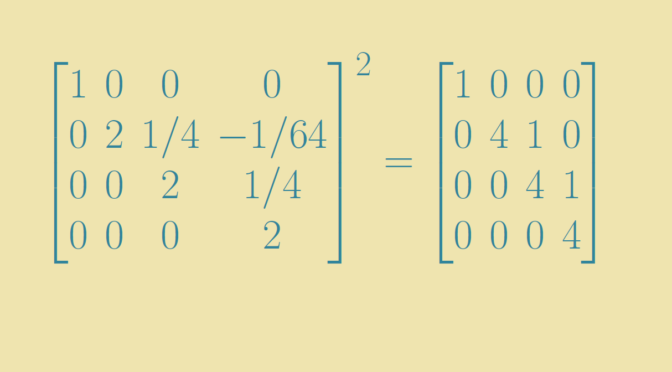Consider for \(n \ge 2\) the linear space \(\mathcal M_n(\mathbb C)\) of complex matrices of dimension \(n \times n\). Is a matrix \(T \in \mathcal M_n(\mathbb C)\) always having a square root \(S \in \mathcal M_n(\mathbb C)\), i.e. a matrix such that \(S^2=T\)? is the question we deal with.

First, one can note that if \(T\) is similar to \(V\) with \(T = P^{-1} V P\) and \(V\) has a square root \(U\) then \(T\) also has a square root as \(V=U^2\) implies \(T=\left(P^{-1} U P\right)^2\).

Diagonalizable matrices

Suppose that \(T\) is similar to a diagonal matrix \[
D=\begin{bmatrix}
d_1 & 0 & \dots & 0 \\
0 & d_2 & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n
\end{bmatrix}\] Any complex number has two square roots, except \(0\) which has only one. Therefore, each \(d_i\) has at least one square root \(d_i^\prime\) and the matrix \[
D^\prime=\begin{bmatrix}
d_1^\prime & 0 & \dots & 0 \\
0 & d_2^\prime & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n^\prime
\end{bmatrix}\] is a square root of \(D\).

Invertible matrices

A complex matrix \(T\) is similar to a matrix \[
J=\begin{bmatrix}
J_1 & & \\
& \ddots &\\
& & J_p
\end{bmatrix}\] where each block \(J_i\) is a square matrix of the form \[
J_i=\begin{bmatrix}
\lambda_i & 1 & &\\
& \lambda_i & \ddots &\\
& & \ddots & 1\\
& & & \lambda_i
\end{bmatrix}\] \(J\) is called the Jordan normal form of \(T\). If \(T\) is supposed to be invertible, the \(\lambda_i\) are non-zero and \(J\) has a square root. For the proof, we prove that a Jordan block \[
J(\lambda)=\begin{bmatrix}
\lambda & 1 & &\\
& \lambda & \ddots &\\
& & \ddots & 1\\
& & & \lambda
\end{bmatrix}\] with \(\lambda \neq 0\) has a square root. Writing \(J(\lambda)= \lambda(I+N)\), where \(N=\frac{J(0)}{\lambda}\) and \(I\) the identity matrix, it is sufficient to prove that \(I+N\) has a square root \(K\) for any nilpotent matrix \(N\) as then \(cK\) is a square root of \(J(\lambda)\) for \(c\) a square root of \(\lambda\).

Recall the Taylor expansion of \(\sqrt{1+x}\) \[
\sqrt{1+x} = 1 + \frac{1}{2} x + \frac{\left(\frac{1}{2}\right)\left(\frac{-1}{2}\right)}{2!} x^2 + \dots + \frac{\left(\frac{1}{2}\right)\left(\frac{-1}{2}\right)\dots \left(\frac{1}{2}-(n-1)\right)}{n!} x^n + \dots\] Plug in \(N\) for \(x\), we get a finite sum as \(N\) is nilpotent. Squaring both side of the equality we get that \[
I+N=\left[1 + \frac{1}{2} N + \frac{\left(\frac{1}{2}\right)\left(\frac{-1}{2}\right)}{2!} N^2 + \dots + \frac{\left(\frac{1}{2}\right)\left(\frac{-1}{2}\right)\dots \left(\frac{1}{2}-(n-1)\right)}{n!} N^n\right]^2\] concluding the proof.

Singular matrices

The case of singular matrices is more complex. For example the matrix \[
A=\begin{bmatrix}
1 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{bmatrix}\] has infinitely many square roots including the matrices \[
A^\prime_t=\begin{bmatrix}
1 & 0 & 0\\
0 & 0 & t\\
0 & 0 & 0\end{bmatrix}\] for \(t \in \mathbb C\).

However the nilpotent matrix \[
B=\begin{bmatrix}
0 & 1\\
0 & 0
\end{bmatrix}\] doesn’t have a square root. Indeed, if \(B^\prime\) was a square root of \(B\), \(B^\prime\) would also be nilpotent and therefore be similar to \(B\) or the zero matrix using the Jordan canonical form of \(B^\prime\). However both squares of those matrices are equal to the zero matrix.