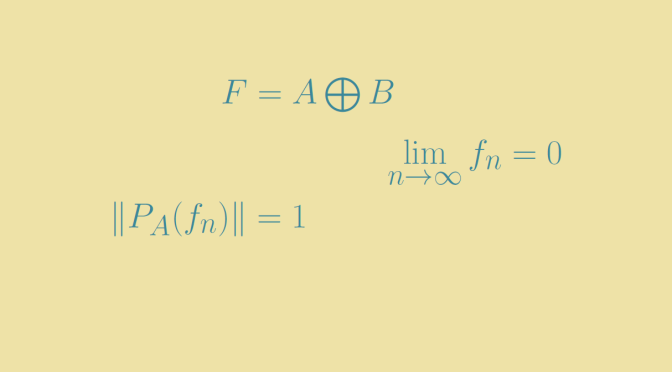Tag Archives: continuity

Analysis

Continuity versus uniform continuity

Leave a comment

We consider real-valued functions.

A real-valued function \(f : I \to \mathbb R\) (where \(I \subseteq\) is an interval) is continuous at \(x_0 \in I\) when: \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x \in I)(\vert x- x_0 \vert \le \delta \Rightarrow \vert f(x)- f(x_0) \vert \le \epsilon).\] When \(f\) is continuous at all \(x \in I\), we say that \(f\) is continuous on \(I\).

\(f : I \to \mathbb R\) is said to be uniform continuity on \(I\) if \[(\forall \epsilon > 0) (\exists \delta > 0)(\forall x,y \in I)(\vert x- y \vert \le \delta \Rightarrow \vert f(x)- f(y) \vert \le \epsilon).\]

Obviously, a function which is uniform continuous on \(I\) is continuous on \(I\). Is the converse true? The answer is negative.

An (unbounded) continuous function which is not uniform continuous

The map \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is continuous. Let’s prove that it is not uniform continuous. For \(0 < x < y\) we have \[\vert f(x)-f(y) \vert = y^2-x^2 = (y-x)(y+x) \ge 2x (y-x)\] Hence for \(y-x= \delta >0\) and \(x = \frac{1}{\delta}\) we get
\[\vert f(x) -f(y) \vert \ge 2x (y-x) =2 > 1\] which means that the definition of uniform continuity is not fulfilled for \(\epsilon = 1\).

For this example, the function is unbounded as \(\lim\limits_{x \to \infty} x^2 = \infty\). Continue reading Continuity versus uniform continuity →

Analysis

Continuity under the integral sign

Leave a comment

We consider here a measure space \((\Omega, \mathcal A, \mu)\) and \(T \subset \mathbb R\) a topological subspace. For a map \(f : T \times \Omega \to \mathbb R\) such that for all \(t \in T\) the map \[
\begin{array}{l|rcl}
f(t, \cdot) : & \Omega & \longrightarrow & \mathbb R \\
& \omega & \longmapsto & f(t,\omega) \end{array}
\] is integrable, one can define the function \[
\begin{array}{l|rcl}
F : & T & \longrightarrow & \mathbb R \\
& t & \longmapsto & \int_\Omega f(t,\omega) \ d\mu(\omega) \end{array}
\]

Following theorem is well known (and can be proven using dominated convergence theorem):

THEOREM for an adherent point \(x \in T\), if

  • \(\forall \omega \in \Omega \lim\limits_{t \to x} f(t,\omega) = \varphi(\omega)\)
  • There exists a map \(g : \Omega \to \mathbb R\) such that \(\forall t \in T, \, \forall \omega \in \Omega, \ \vert f(t,\omega) \vert \le g(\omega)\)

then \(\varphi\) is integrable and \[
\lim\limits_{t \to x} F(t) = \int_\Omega \varphi(\omega) \ d\mu(\omega)\]
In other words, one can switch \(\lim\) and \(\int\) signs.

We provide here a counterexample showing that the conclusion of the theorem might not hold if \(f\) is not bounded by a function \(g\) as supposed in the premises of the theorem. Continue reading Continuity under the integral sign →

Analysis

Counterexamples around Dini’s theorem

Leave a comment

In this article we look at counterexamples around Dini’s theorem. Let’s recall:

Dini’s theorem: If \(K\) is a compact topological space, and \((f_n)_{n \in \mathbb N}\) is a monotonically decreasing sequence (meaning \(f_{n+1}(x) \le f_n(x)\) for all \(n \in \mathbb N\) and \(x \in K\)) of continuous real-valued functions on \(K\) which converges pointwise to a continuous function \(f\), then the convergence is uniform.

We look at what happens to the conclusion if we drop some of the hypothesis.

Cases if \(K\) is not compact

We take \(K=(0,1)\), which is not closed equipped with the common distance. The sequence \(f_n(x)=x^n\) of continuous functions decreases pointwise to the always vanishing function. But the convergence is not uniform because for all \(n \in \mathbb N\) \[\sup\limits_{x \in (0,1)} x^n = 1\]

The set \(K=\mathbb R\) is closed but unbounded, hence also not compact. The sequence defined by \[f_n(x)=\begin{cases}
0 & \text{for } x < n\\ \frac{x-n}{n} & \text{for } n \le x < 2n\\ 1 & \text{for } x \ge 2n \end{cases}\] is continuous and monotonically decreasing. It converges to \(0\). However, the convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in \mathbb R\} =1\). Continue reading Counterexamples around Dini’s theorem →

Topology

Counterexamples around Banach-Steinhaus theorem

Leave a comment

In this article we look at what happens to Banach-Steinhaus theorem when the completness hypothesis is not fulfilled. One form of Banach-Steinhaus theorem is the following one.

Banach-Steinhaus Theorem Let \(T_n : E \to F\) be a sequence of continuous linear maps from a Banach space \(E\) to a normed space \(F\). If for all \(x \in E\) the sequence \(T_n x\) is convergent to \(Tx\), then \(T\) is a continuous linear map.

A sequence of continuous linear maps converging to an unbounded linear map

Let \(c_{00}\) be the vector space of real sequences \(x=(x_n)\) eventually vanishing, equipped with the norm \[\Vert x \Vert = \sup_{n \in \mathbb N} \vert x_n \vert\] For \(n \in \mathbb N\), \(T_n : E \to E\) denotes the linear map defined by \[T_n x = (x_1,2 x_2, \dots, n x_n,0,0, \dots).\] \(T_n\) is continuous as for \(\Vert x \Vert \le 1\), we have
\begin{align*}
\Vert T_n x \Vert &= \Vert (x_1,2 x_2, \dots, n x_n,0,0, \dots) \Vert\\
& = \sup_{1 \le k \le n} \vert k x_k \vert \le n \Vert x \Vert \le n
\end{align*} Continue reading Counterexamples around Banach-Steinhaus theorem →

Analysis

A discontinuous real convex function

Leave a comment

Consider a function \(f\) defined on a real interval \(I \subset \mathbb R\). \(f\) is called convex if: \[\forall x, y \in I \ \forall \lambda \in [0,1]: \ f((1-\lambda)x+\lambda y) \le (1-\lambda) f(x) + \lambda f(y)\]

Suppose that \(I\) is a closed interval: \(I=[a,b]\) with \(a < b\). For \(a < s < t < u < b\) one can prove that: \[\frac{f(t)-f(s)}{t-s}\le \frac{f(u)-f(s)}{u-s}\le\frac{f(u)-f(t)}{u-t}.\] It follows from those relations that \(f\) has left-hand and right-hand derivatives at each point of the interior of \(I\). And therefore that \(f\) is continuous at each point of the interior of \(I\).
Is a convex function defined on an interval \(I\) continuous at all points of the interval? That might not be the case and a simple example is the function: \[\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & \mathbb R \\
& x & \longmapsto & 0 \text{ for } x \in (0,1) \\
& x & \longmapsto & 1 \text{ else}\end{array}\]

It can be easily verified that \(f\) is convex. However, \(f\) is not continuous at \(0\) and \(1\).

Analysis

Continuity of multivariable real functions

1 Comment

This article provides counterexamples about continuity of functions of several real variables. In addition the article discusses the cases of functions of two real variables (defined on \(\mathbb R^2\) having real values. \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall that a function \(f\) defined from \(\mathbb R^2\) to \(\mathbb R\) is continuous at \((x_0,y_0) \in \mathbb R^2\) if for any \(\epsilon > 0\), there exists \(\delta > 0\), such that \(\Vert (x,y) -(x_0,y_0) \Vert < \delta \Rightarrow \vert f(x,y) - f(x_0,y_0) \vert < \epsilon\). Continue reading Continuity of multivariable real functions →

Topology

Two algebraically complemented subspaces that are not topologically complemented

Leave a comment

We give here an example of a two complemented subspaces \(A\) and \(B\) that are not topologically complemented.

For this, we consider a vector space of infinite dimension equipped with an inner product. We also suppose that \(E\) is separable. Hence, \(E\) has an orthonormal basis \((e_n)_{n \in \mathbb N}\).

Let \(a_n=e_{2n}\) and \(b_n=e_{2n}+\frac{1}{2n+1} e_{2n+1}\). We denote \(A\) and \(B\) the closures of the linear subspaces generated by the vectors \((a_n)\) and \((b_n)\) respectively. We consider \(F=A+B\) and prove that \(A\) and \(B\) are complemented subspaces in \(F\), but not topologically complemented. Continue reading Two algebraically complemented subspaces that are not topologically complemented →

Analysis

Counterexamples on function limits (part 1)

Leave a comment

Let \(f\) and \(g\) be two real functions and \(a \in \mathbb R \cup \{+\infty\}\). We provide here examples and counterexamples regarding the limits of \(f\) and \(g\).

If \(f\) has a limit as \(x\) tends to \(a\) then \(\vert f \vert\) also?

This is true. It is a consequence of the reverse triangle inequality \[\left\vert \vert f(x) \vert – \vert l \vert \right\vert \le \vert f(x) – l \vert\] Hence if \(\displaystyle \lim\limits_{x \to a} f(x) = l\), \(\displaystyle \lim\limits_{x \to a} \vert f(x) \vert = \vert l \vert\)

Is the converse of previous statement also true?

It is not. Consider the function defined by: \[\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& \frac{1}{n} & \longmapsto & -1 \text{ for } n \ge 1 \text{ integer} \\
& x & \longmapsto & 1 \text{ otherwise} \end{array}\] \(\vert f \vert\) is the constant function equal to \(1\), hence \(\vert f \vert\) has \(1\) for limit as \(x\) tends to zero. However \(\lim\limits_{x \to 0} f(x)\) doesn’t exist. Continue reading Counterexamples on function limits (part 1) →

Topology

A homeomorphism of the unit ball having no fixed point

Leave a comment

Let’s recall Brouwer fixed-point theorem.

Theorem (Brouwer): Every continuous function from a convex compact subset \(K\) of a Euclidean space to \(K\) itself has a fixed point.

We here describe an example of a homeomorphism of the unit ball of a Hilbert space having no fixed point. Let \(E\) be a separable Hilbert space with \((e_n)_{n \in \mathbb{Z}}\) as a Hilbert basis. \(B\) and \(S\) are respectively \(E\) closed unit ball and unit sphere.

There is a unique linear map \(u : E \to E\) for which \(u(e_n)=e_{n+1}\) for all \(n \in \mathbb{Z}\). For \(x = \sum_{n \in \mathbb{Z}} \xi_n e_n \in E\) we have \(u(x)= \sum_{n \in \mathbb{Z}} \xi_n e_{n+1}\). \(u\) is isometric as \[\Vert u(x) \Vert^2 = \sum_{n \in \mathbb{Z}} \vert \xi_n \vert^2 = \Vert x \Vert^2\] hence one-to-one. \(u\) is also onto as for \(x = \sum_{n \in \mathbb{Z}} \xi_n e_n \in E\), \(\sum_{n \in \mathbb{Z}} \xi_n e_{n-1} \in E\) is an inverse image of \(x\). Finally \(u\) is an homeomorphism. Continue reading A homeomorphism of the unit ball having no fixed point →

Analysis

Pointwise convergence and properties of the limit (part 1)

Leave a comment

We look here at the continuity of a sequence of functions that converges pointwise and give some counterexamples of what happens versus uniform convergence.

Recalling the definition of pointwise convergence

We consider here real functions defined on a closed interval \([a,b]\). A sequence of functions \((f_n)\) defined on \([a,b]\) converges pointwise to the function \(f\) if and only if for all \(x \in [a,b]\) \(\displaystyle \lim\limits_{n \to +\infty} f_n(x) = f(x)\). Pointwise convergence is weaker than uniform convergence.

Pointwise convergence does not, in general, preserve continuity

Suppose that \(f_n \ : \ [0,1] \to \mathbb{R}\) is defined by \(f_n(x)=x^n\). For \(0 \le x <1\) then \(\displaystyle \lim\limits_{n \to +\infty} x^n = 0\), while if \(x = 1\) then \(\displaystyle \lim\limits_{n \to +\infty} x^n = 1\). Hence the sequence \(f_n\) converges to the function equal to \(0\) for \(0 \le x < 1\) and to \(1\) for \(x=1\). Although each \(f_n\) is a continuous function of \([0,1]\), their pointwise limit is not. \(f\) is discontinuous at \(1\). We notice that \((f_n)\) doesn't converge uniformly to \(f\) as for all \(n \in \mathbb{N}\), \(\displaystyle \sup\limits_{x \in [0,1]} \vert f_n(x) - f(x) \vert = 1\). That's reassuring as uniform convergence of a sequence of continuous functions implies that the limit is continuous! Continue reading Pointwise convergence and properties of the limit (part 1) →