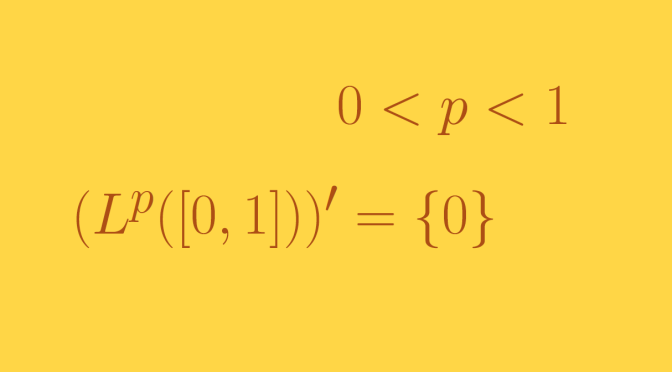We consider here the \(L^p\)- spaces of real functions defined on \([0,1]\) for which the \(p\)-th power of the absolute value is Lebesgue integrable. We focus on the case \(0 < p < 1\). We'll prove that those \(L^p\)-spaces are topological vector spaces on which there exists no continuous non-trivial linear forms (i.e. not vanishing identically). Continue reading A topological vector space with no non trivial continuous linear form
Tag Archives: continuity
A nowhere locally bounded function
In that article, I described some properties of Thomae’s function\(f\). Namely:
- The function is discontinuous on \(\mathbb{Q}\).
- Continuous on \(\mathbb{R} \setminus \mathbb{Q}\).
- Its right-sided and left-sided limits vanish at all points.
Let’s modify \(f\) to get function \(g\) defined as follow:
\[g:
\left|\begin{array}{lrl}
\mathbb{R} & \longrightarrow & \mathbb{R} \\
x & \longmapsto & 0 \text{ if } x \in \mathbb{R} \setminus \mathbb{Q} \\
\frac{p}{q} & \longmapsto & q \text{ if } \frac{p}{q} \text{ in lowest terms and } q > 0
\end{array}\right.\] \(f\) and \(g\) both vanish on the set of irrational numbers, while on the set of rational numbers, \(g\) is equal to the reciprocal of \(f\). We now consider an open subset \(O \subset \mathbb{R}\) and \(x \in O\). As \(f\) right-sided and left-sided limits vanish at all points, we have \(\lim\limits_{n \to +\infty} f(x_n) = 0\) for all sequence \((x_n)\) of rational numbers converging to \(x\) (and such a sequence exists as the rational numbers are everywhere dense in the reals). Hence \(\lim\limits_{n \to +\infty} g(x_n) = + \infty\) as \(f\) is positive.
We can conclude that \(g\) is nowhere locally bounded. The picture of the article is a plot of function \(g\) on the rational numbers \(r = \frac{p}{q}\) in lowest terms for \(0 < r < 1\) and \(q \le 50\).
A function continuous at all irrationals and discontinuous at all rationals
Let’s discover the beauties of Thomae’s function also named the popcorn function, the raindrop function or the modified Dirichlet function.
Thomae’s function is a real-valued function defined as:
\[f:
\left|\begin{array}{lrl}
\mathbb{R} & \longrightarrow & \mathbb{R} \\
x & \longmapsto & 0 \text{ if } x \in \mathbb{R} \setminus \mathbb{Q} \\
\frac{p}{q} & \longmapsto & \frac{1}{q} \text{ if } \frac{p}{q} \text{ in lowest terms and } q > 0
\end{array}\right.\]
\(f\) is periodic with period \(1\)
This is easy to prove as for \(x \in \mathbb{R} \setminus \mathbb{Q}\) we also have \(x+1 \in \mathbb{R} \setminus \mathbb{Q}\) and therefore \(f(x+1)=f(x)=0\). While for \(y=\frac{p}{q} \in \mathbb{Q}\) in lowest terms, \(y+1=\frac{p+q}{q}\) is also in lowest terms, hence \(f(y+1)=f(y)=\frac{1}{q}\). Continue reading A function continuous at all irrationals and discontinuous at all rationals
Two continuous bijections but no homeomorphism
We consider here two topological spaces \(X\) and \(Y\). We also suppose that \(f\) is a continuous bijection from \(X\) to \(Y\) and \(g\) a continuous bijection from \(Y\) to \(X\). Providing such hypothesis (H), is there necessarily an homeomorphism from \(X\) to \(Y\)? Continue reading Two continuous bijections but no homeomorphism
Continuous maps that are not closed or not open
We recall some definitions on open and closed maps. In topology an open map is a function between two topological spaces which maps open sets to open sets. Likewise, a closed map is a function which maps closed sets to closed sets.
For a continuous function \(f: X \mapsto Y\), the preimage \(f^{-1}(V)\) of every open set \(V \subseteq Y\) is an open set which is equivalent to the condition that the preimages of the closed sets (which are the complements of the open subsets) in \(Y\) are closed in \(X\). However, a continuous function might not be an open map or a closed map as we prove in following counterexamples. Continue reading Continuous maps that are not closed or not open
A continuous function not differentiable at the rationals but differentiable elsewhere
We build here a continuous function of one real variable whose derivative exists on \(\mathbb{R} \setminus \mathbb{Q}\) and doesn’t have a left or right derivative on each point of \(\mathbb{Q}\).
As \(\mathbb{Q}\) is (infinitely) countable, we can find a bijection \(n \mapsto r_n\) from \(\mathbb{N}\) to \(\mathbb{Q}\). We now reuse the function \(f\) defined here. Recall \(f\) main properties: Continue reading A continuous function not differentiable at the rationals but differentiable elsewhere
A differentiable function except at one point with a bounded derivative
We build here a continuous function of one real variable whose derivative exists except at \(0\) and is bounded on \(\mathbb{R^*}\).
We start with the even and piecewise linear function \(g\) defined on \([0,+\infty)\) with following values:
\[g(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x =0\\
0 & \mbox{if } x \in \{\frac{k}{4^n};(k,n) \in \{1,2,4\} \times \mathbb{N^*}\}\\
1 & \mbox{if } x \in \{\frac{3}{4^n};n \in \mathbb{N^*}\}\\
\end{array}
\right.
\]
The picture below gives an idea of the graph of \(g\) for positive values. Continue reading A differentiable function except at one point with a bounded derivative
A continuous function which is not of bounded variation
Introduction on total variation of functions
Recall that a function of bounded variation, also known as a BV-function, is a real-valued function whose total variation is bounded (finite).
Being more formal, the total variation of a real-valued function \(f\), defined on an interval \([a,b] \subset \mathbb{R}\) is the quantity:
\[V_a^b(f) = \sup\limits_{P \in \mathcal{P}} \sum_{i=0}^{n_P-1} \left\vert f(x_{i+1}) – f(x_i) \right\vert\] where the supremum is taken over the set \(\mathcal{P}\) of all partitions of the interval considered. Continue reading A continuous function which is not of bounded variation
A function that is everywhere continuous and nowhere differentiable
Let \(f_1(x) = |x|\) for \(| x | \le \frac{1}{2}\), and let \(f_1\) be defined for other values of \(x\) by periodic continuation with period \(1\). \(f_1\) graph looks like following picture:
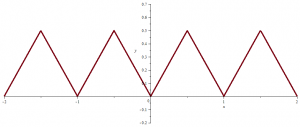
\(f_1\) is continuous everywhere and differentiable on \(\mathbb{R} \setminus \mathbb{Z}\). Continue reading A function that is everywhere continuous and nowhere differentiable
A nowhere continuous function
This is a strange function!
One example is the Dirichlet function \(1_{\mathbb{Q}}\).
\(1_{\mathbb{Q}}(x)=1\) if \(x \in \mathbb{Q}\) and
\(1_{\mathbb{Q}}(x)=0\) if \(x \in \mathbb{R} \setminus \mathbb{Q}\).
\(1_{\mathbb{Q}}\) is everywhere discontinuous because \(\mathbb{Q}\) is everywhere dense in \(\mathbb{R}\).
The function \(x \mapsto x \cdot 1_{\mathbb{Q}}(x)\) is continuous in \(0\) and discontinuous elsewhere.