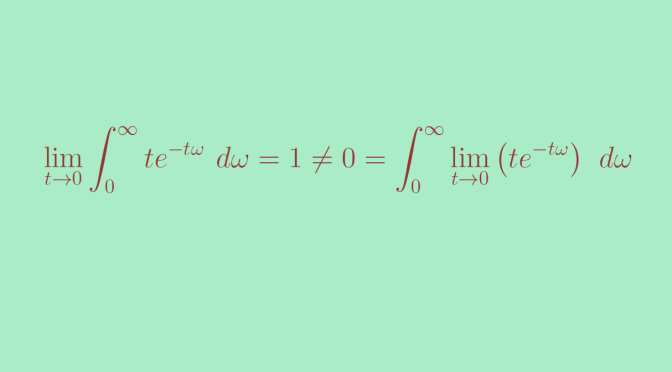We consider here a measure space \((\Omega, \mathcal A, \mu)\) and \(T \subset \mathbb R\) a topological subspace. For a map \(f : T \times \Omega \to \mathbb R\) such that for all \(t \in T\) the map \[
\begin{array}{l|rcl}
f(t, \cdot) : & \Omega & \longrightarrow & \mathbb R \\
& \omega & \longmapsto & f(t,\omega) \end{array}
\] is integrable, one can define the function \[
\begin{array}{l|rcl}
F : & T & \longrightarrow & \mathbb R \\
& t & \longmapsto & \int_\Omega f(t,\omega) \ d\mu(\omega) \end{array}
\]

Following theorem is well known (and can be proven using dominated convergence theorem):

THEOREM for an adherent point \(x \in T\), if

• \(\forall \omega \in \Omega \lim\limits_{t \to x} f(t,\omega) = \varphi(\omega)\)
• There exists a map \(g : \Omega \to \mathbb R\) such that \(\forall t \in T, \, \forall \omega \in \Omega, \ \vert f(t,\omega) \vert \le g(\omega)\)

then \(\varphi\) is integrable and \[
\lim\limits_{t \to x} F(t) = \int_\Omega \varphi(\omega) \ d\mu(\omega)\]
In other words, one can switch \(\lim\) and \(\int\) signs.

We provide here a counterexample showing that the conclusion of the theorem might not hold if \(f\) is not bounded by a function \(g\) as supposed in the premises of the theorem.

Let’s consider \[
\begin{array}{l|rcl}
f : & [0, \infty) \times [0, \infty) & \longrightarrow & \mathbb R \\
& (t, \omega) & \longmapsto & t e^{-t \omega} \end{array}
\] For all \(t \in [0,\infty)\), the map \(\omega \mapsto f(t,\omega)\) is integrable on \([0, \infty)\). Therefore, one can define \[
\begin{array}{l|rcl}
F : & [0, \infty) & \longrightarrow & \mathbb R \\
& t & \longmapsto & \int_0^\infty t e^{-t \omega} \ d\omega\end{array}
\]

Moreover for all \(\omega \in [0,\infty)\), \(f(0,\omega)=0\) hence \(F(0)=0\). And for \(t \neq 0\), \[
F(t)=\int_0^\infty t e^{-t \omega} \ d\omega = 1.\]

Finally \[
\lim\limits_{t \to 0} \int_0^\infty t e^{-t \omega} \ d\omega = 1 \neq 0 = \int_0^\infty \lim\limits_{t \to 0} \left( t e^{-t \omega} \right) \ d\omega\]

One can verify that for \(\omega \in (0,\infty)\), the maximum of \(t \mapsto t e^{-t \omega}\) is obtained for \(t = \frac{1}{\omega}\) and is equal to \(\frac{1}{e \omega}\). Hence a map \(g\) as defined in the hypotheses of the theorem is forced to satisfy the inequality \(\frac{1}{e \omega} \le g(\omega)\) and cannot be integrable.