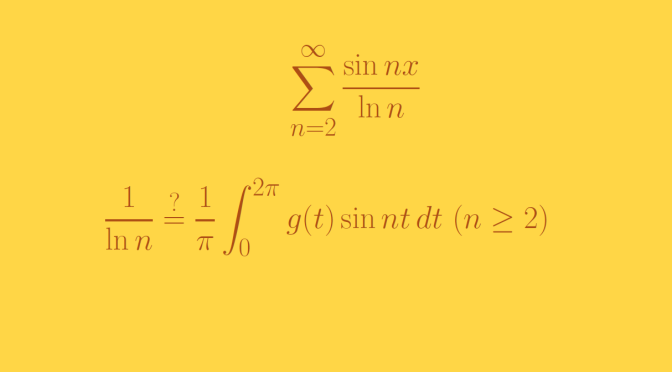We already provided here an example of a trigonometric series that is not the Fourier series of a Riemann-integrable function (namely the function \(\displaystyle x \mapsto \sum_{n=1}^\infty \frac{\sin nx}{\sqrt n}\)).
Applying an Abel-transformation (like mentioned in the link above), one can see that the function \[f(x)=\sum_{n=2}^\infty \frac{\sin nx}{\ln n}\] is everywhere convergent. We now prove that \(f\) cannot be the Fourier series of a Lebesgue-integrable function. The proof is based on the fact that for a \(2 \pi\)-periodic function \(g\), Lebesgue-integrable on \([0,2 \pi]\), the sum \[\sum_{n=1}^\infty \frac{c_n-c_{-n}}{n}\] is convergent where \((c_n)_{n \in \mathbb Z}\) are the complex Fourier coefficients of \(g\): \[c_n = \frac{1}{2 \pi} \int_0^{2 \pi} g(t)e^{-ikt} \ dt.\] As the series \(\displaystyle \sum_{n=2}^\infty \frac{1}{n \ln n}\) is divergent, we will be able to conclude that the sequence defined by \[\gamma_0=\gamma_1=\gamma_{-1} = 0, \, \gamma_n=- \gamma_{-n} = \frac{1}{\ln n} \ (n \ge 2)\] cannot be the Fourier coefficients of a Lebesgue-integrable function, hence that \(f\) is not the Fourier series of any Lebesgue-integrable function.
So we’re reduce to prove the following lemma:
LEMMA: for a \(2 \pi\)-periodic function \(g\), Lebesgue-integrable on \([0,2 \pi]\), the sum \[\sum_{n=1}^\infty \frac{c_n-c_{-n}}{n}\] is convergent.
We have for \(n \ge 1\): \[\sum_{k=1}^n \frac{c_k-c_{-k}}{k} = – \frac{i}{\pi} \int_0^{2 \pi} g(x) \sum_{k=1}^n \frac{\sin kx}{k} \ dx\] If we prove that \[U_n: x \mapsto \sum_{k=1}^n \frac{\sin kx}{k}\] is a pointwise convergent sequence of functions bounded by a constant independent of \(n\) and \(x\), we’ll be done applying Lebesgue dominated convergence theorem.
The pointwise convergence of \((U_n)\) can again be obtained using an Abel transformation. Now, denoting \[D_n(x) = \sum_{k=-n}^n e^{ikx} = \frac{\sin \left((n+\frac{1}{2})x \right )}{\sin \left( \frac{x}{2} \right)},\] we have
\[U_n(x) = \frac{1}{2} \int_0^x (D_n(t) – 1) \ dt.\] Therefore, we’ll be able to conclude if we prove that \(\displaystyle \int_0^x D_n(t) \ dt\) is bounded by a constant independent of \(n\) and \(x\) for \(x \in [0,2 \pi]\). As \(D_n\) is even for all \(n \ge 1\), it is sufficient to consider \(x \in [0, \pi]\).
The map \[t \mapsto \frac{1}{\sin (t/2)} – \frac{1}{t/2}\] defined on \((0,\pi]\) can be extended by continuity to \(0\), which gives a map \(\phi\) defined on \([0,\pi]\) and for \(\alpha \in [0,\pi]\):
\[\left\vert \int_0^\alpha \frac{\sin \left((n+\frac{1}{2})t \right )}{\sin \left( \frac{t}{2} \right)} \ dt – \int_0^\alpha \frac{\sin \left((n+\frac{1}{2})t \right )}{\frac{t}{2}} \ dt\right\vert \le \int_0^\pi \vert \phi(t) \vert \ dt.\] We get the desired conclusion as
\[\int_0^\alpha \frac{\sin \left((n+\frac{1}{2})t \right )}{\frac{t}{2}} \ dt = 2 \int_0^{(n+\frac{1}{2})\alpha} \frac{\sin t}{t} \ dt\] and the integral \(\displaystyle \int_0^\infty \frac{\sin t}{t} \ dt\) is known to be convergent.