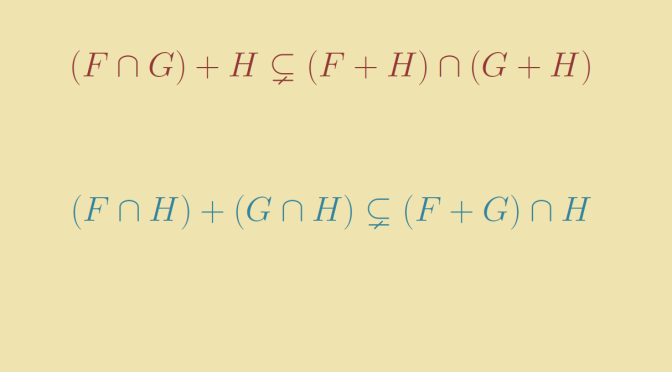Let’s consider a vector space \(E\) over a field \(K\). We’ll look at relations involving basic set operations and sum of subspaces. We denote by \(F, G\) and \(H\) subspaces of \(E\).
The relation \((F \cap G) + H \subset (F+H) \cap (G + H)\)
This relation holds. The proof is quite simple. For any \(x \in (F \cap G) + H\) there exists \(y \in F \cap G\) and \(h \in H\) such that \(x=y+h\). As \(y \in F\), \(x \in F+H\) and by a similar argument \(x \in F+H\). Therefore \(x \in (F+H) \cap (G + H)\).
Is the inclusion \((F \cap G) + H \subset (F+H) \cap (G + H)\) always an equality? The answer is negative. Take for the space \(E\) the real 3 dimensional space \(\mathbb R^3\). And for the subspaces:
- \(H\) the plane of equation \(z=0\),
- \(F\) the line of equations \(y = 0, \, x=z\),
- \(G\) the line of equations \(y = 0, \, x=-z\),
We have \(F+H=G+H=E\), \((F \cap G)=\{0\}\) which leads to \[
H = (F \cap G) + H \subsetneq (F+H) \cap (G + H) = E.\]
The relation \((F \cap H) + (G \cap H) \subset (F+G) \cap H\)
If \(f+g \in (F \cap H) + (G \cap H)\) with \(f,g \in H\) then \(f+g \in F+G\) and \(f+g \in H\) (as \(H\) is a subspace). Hence the inclusion.
Again the inclusion can be strict. In particular this is the case if \(F, G, H\) are 3 distinct lines of the plane \(\mathbb R^2\). In that case \(F \cap H = G \cap H= \{0\}\) while \((F+G) \cap H = H\).