Consider a normed vector space \((X, \Vert \cdot \Vert)\). If \(X\) is finite-dimensional, then a subset \(Y \subset X\) is compact if and only if it is closed and bounded. In particular a closed ball \(B_r[a] = \{x \in X \, ; \, \Vert x – a \Vert \le r\}\) is always compact if \(X\) is finite-dimensional.

What about infinite-dimensional spaces?

The space \(A=C([0,1],\mathbb R)\)

Consider the space \(A=C([0,1],\mathbb R)\) of the real continuous functions defined on the interval \([0,1]\) endowed with the sup norm:
\[\Vert f \Vert = \sup\limits_{x \in [0,1]} \vert f(x) \vert\]
Is the closed unit ball \(B_1[0]\) compact? The answer is negative and we provide two proofs.

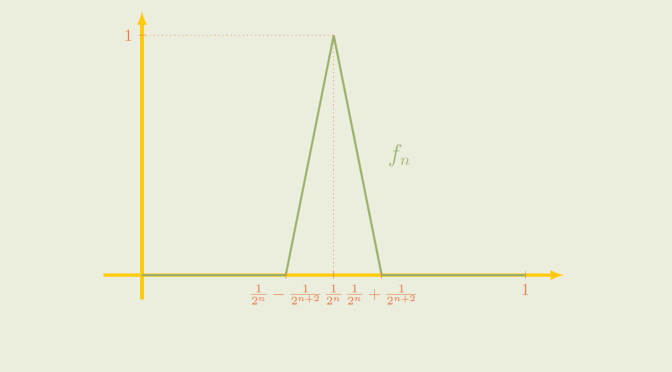
The first one is based on open covers. For \(n \ge 1\), we denote by \(f_n\) the piecewise linear map defined by \[
\begin{cases}
f_n(0)=f_n(\frac{1}{2^n}-\frac{1}{2^{n+2}})=0 \\
f_n(\frac{1}{2^n})=1 \\
f_n(\frac{1}{2^n}+\frac{1}{2^{n+2}})=f_n(1)=0
\end{cases}\] All the \(f_n\) belong to \(B_1[0]\). Moreover for \(1 \le n < m\) we have \(\frac{1}{2^n}+\frac{1}{2^{n+2}} < \frac{1}{2^m}-\frac{1}{2^{m+2}}\). Hence the supports of the \(f_n\) are disjoint and \(\Vert f_n – f_m \Vert = 1\).

Now consider the open cover \(\mathcal U=\{B_{\frac{1}{2}}(x) \, ; \, x \in B_1[0]\}\). For \(x \in B_1[0]\}\) and \(u,v \in B_{\frac{1}{2}}(x)\), \(\Vert u -v \Vert < 1\). Therefore, each \(B_{\frac{1}{2}}(x)\) contains at most one \(f_n\) and a finite subcover of \(\mathcal U\) will contain only a finite number of \(f_n\) proving that \(A\) is not compact.

Second proof based on convergent subsequence. As \(A\) is a metric space, it is enough to prove that \(A\) is not sequentially compact. Consider the sequence of functions \(g_n : x \mapsto x^n\). The sequence is bounded as for all \(n \in \mathbb N\), \(\Vert g_n \Vert = 1\). If \((g_n)\) would have a convergent subsequence, the subsequence would converge pointwise to the function equal to \(0\) on \([0,1)\) and to \(1\) at \(1\). As this function is not continuous, \((g_n)\) cannot have a subsequence converging to a map \(g \in A\).

Riesz’s theorem

The non-compactness of \(A=C([0,1],\mathbb R)\) is not so strange. Based on Riesz’s lemma one can show that the unit ball of an infinite-dimensional normed space \(X\) is never compact. This is sometimes known as the Riesz’s theorem.

The non-compactness of \(A=C([0,1],\mathbb R)\) is just standard for infinite-dimensional normed vector spaces!