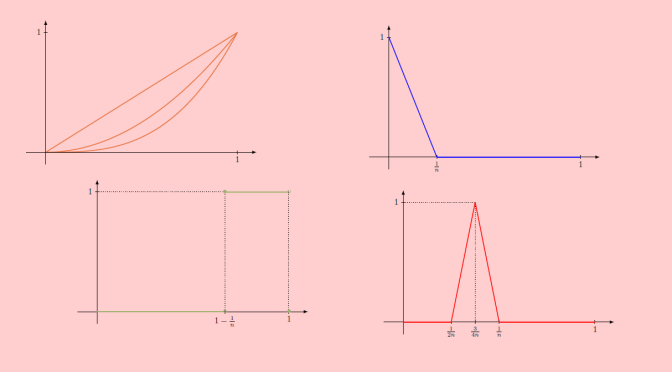
In this article we look at counterexamples around Dini’s theorem. Let’s recall:
Dini’s theorem: If \(K\) is a compact topological space, and \((f_n)_{n \in \mathbb N}\) is a monotonically decreasing sequence (meaning \(f_{n+1}(x) \le f_n(x)\) for all \(n \in \mathbb N\) and \(x \in K\)) of continuous real-valued functions on \(K\) which converges pointwise to a continuous function \(f\), then the convergence is uniform.
We look at what happens to the conclusion if we drop some of the hypothesis.
Cases if \(K\) is not compact
We take \(K=(0,1)\), which is not closed equipped with the common distance. The sequence \(f_n(x)=x^n\) of continuous functions decreases pointwise to the always vanishing function. But the convergence is not uniform because for all \(n \in \mathbb N\) \[\sup\limits_{x \in (0,1)} x^n = 1\]
The set \(K=\mathbb R\) is closed but unbounded, hence also not compact. The sequence defined by \[f_n(x)=\begin{cases}
0 & \text{for } x < n\\
\frac{x-n}{n} & \text{for } n \le x < 2n\\
1 & \text{for } x \ge 2n
\end{cases}\]
is continuous and monotonically decreasing. It converges to \(0\). However, the convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in \mathbb R\} =1\).
Counterexample if \(f\) is not continuous
We take \(K=[0,1]\) which is compact and the sequence \[f_n(x)=\begin{cases}
1 – 2nx & \text{for } 0 \le x < \frac{1}{2n}\\
0 & \text{for } \frac{1}{2n} \le x \le 1
\end{cases}\] One can verify that \(f_n\) is continuous for all \(n \in \mathbb N\). The sequence \((f_n)\) is decreasing and converges pointwise to the discontinuous function equal to \(1\) at \(0\) and to \(0\) elsewhere. However, again the convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in [0,1]\} =1\).
Counterexample if \((f_n)\) is not monotonically increasing or decreasing
We keep \(K=[0,1]\) and consider the sequence \[f_n(x)=\begin{cases}
0 & \text{for } 0 \le x < \frac{1}{2n}\\
4nx-2 & \text{for } \frac{1}{2n} \le x < \frac{3}{4n}\\
4-4nx & \frac{3}{4n} \le x < \frac{1}{n}\\
1 & \text{for } \frac{1}{n} \le x \le 1
\end{cases}\] One can verify that \(f_n\) is continuous for all \(n \in \mathbb N\). The sequence \((f_n)\) converges pointwise to \(0\). However, again the convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in [0,1]\} =1\).
Counterexample if the \(f_n\) are not continuous
We consider again \(K=[0,1]\) and the sequence \[f_n(x)=\begin{cases}
0 & \text{for } 0 \le x < 1-{1\over n}\\
1 & \text{for } 1-{1\over n} \le x < 1\\
0 & \text{for } x=1
\end{cases}\] \((f_n)\) is a sequence of non continuous functions, converging pointwise to \(0\). The convergence is not uniform as for all \(n \in \mathbb N\): \(\sup\{f_n(x) : x \in [0,1]\} =1\).