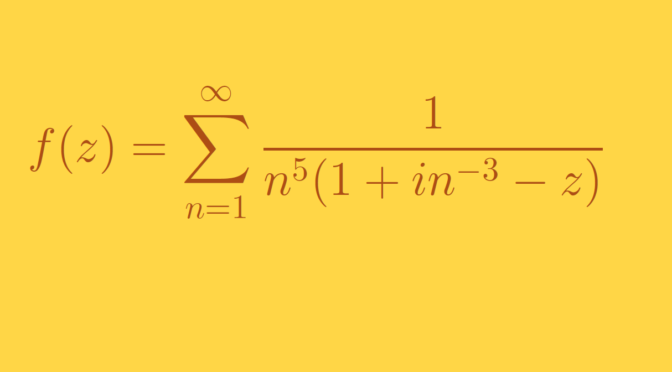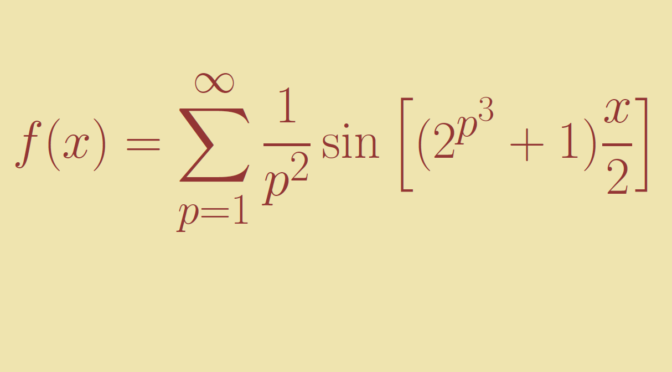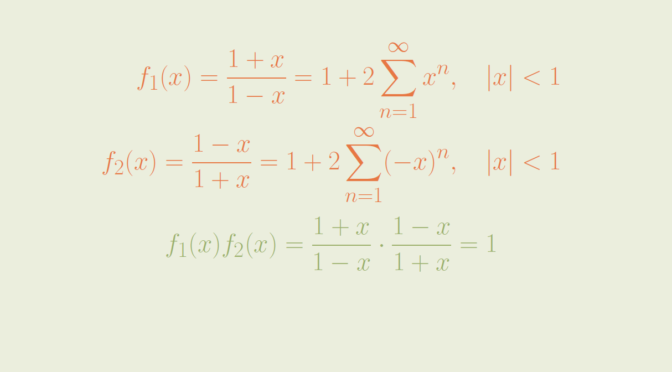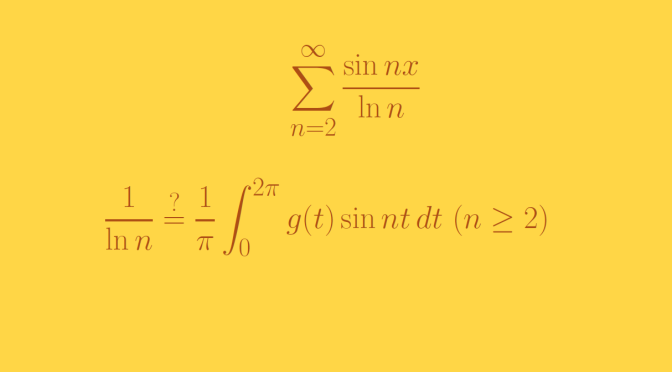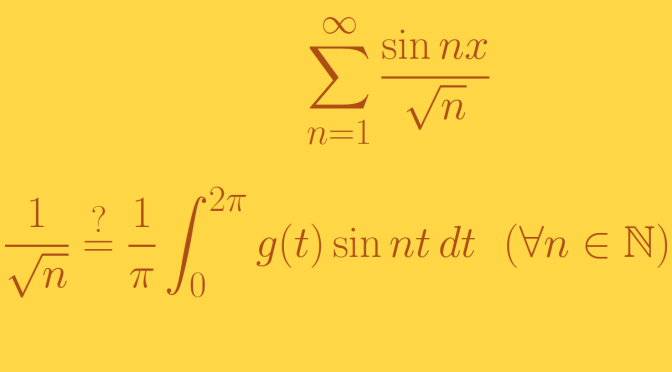Let’s start by recalling an important theorem of real analysis:
THEOREM. A necessary and sufficient condition for the convergence of a real sequence is that it is bounded and has a unique limit point.
As a consequence of the theorem, a sequence having a unique limit point is divergent if it is unbounded. An example of such a sequence is the sequence \[
u_n = \frac{n}{2}(1+(-1)^n),\] whose initial values are \[
0, 1, 0, 2, 0, 3, 0, 4, 0, 5, 6, \dots\] \((u_n)\) is an unbounded sequence whose unique limit point is \(0\).
Let’s now look at sequences having more complicated limit points sets.
A sequence whose set of limit points is the set of natural numbers
Consider the sequence \((v_n)\) whose initial terms are \[
1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, \dots\] \((v_n)\) is defined as follows \[
v_n=\begin{cases}
1 &\text{ for } n= 1\\
n – \frac{k(k+1)}{2} &\text{ for } \frac{k(k+1)}{2} \lt n \le \frac{(k+1)(k+2)}{2}
\end{cases}\] \((v_n)\) is well defined as the sequence \((\frac{k(k+1)}{2})_{k \in \mathbb N}\) is strictly increasing with first term equal to \(1\). \((v_n)\) is a sequence of natural numbers. As \(\mathbb N\) is a set of isolated points of \(\mathbb R\), we have \(V \subseteq \mathbb N\), where \(V\) is the set of limit points of \((v_n)\). Conversely, let’s take \(m \in \mathbb N\). For \(k + 1 \ge m\), we have \(\frac{k(k+1)}{2} + m \le \frac{(k+1)(k+2)}{2}\), hence \[
u_{\frac{k(k+1)}{2} + m} = m\] which proves that \(m\) is a limit point of \((v_n)\). Finally the set of limit points of \((v_n)\) is the set of natural numbers.