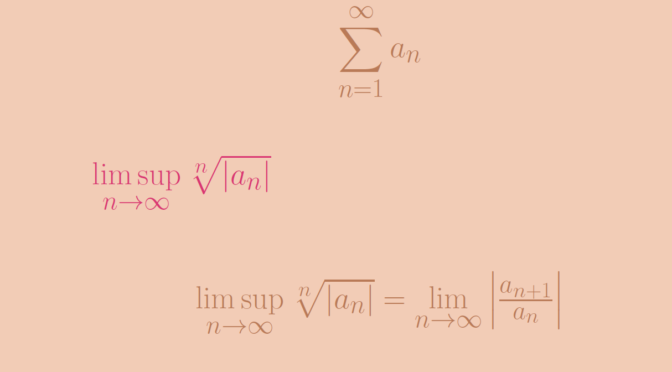The root test is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number. The root test was developed first by Augustin-Louis Cauchy.

We denote \[l = \limsup\limits_{n \to \infty} \sqrt[n]{\vert a_n \vert}.\] \(l\) is a non-negative real number or is possibly equal to \(\infty\). The root test states that:

• if \(l < 1\) then the series converges absolutely;
• if \(l > 1\) then the series diverges.

The root test is inconclusive when \(l = 1\).

A case where \(l=1\) and the series diverges

The harmonic series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n}\) is divergent. However \[\sqrt[n]{\frac{1}{n}} = \frac{1}{n^{\frac{1}{n}}}=e^{- \frac{1}{n} \ln n} \] and \(\limsup\limits_{n \to \infty} \sqrt[n]{\frac{1}{n}} = 1\) as \(\lim\limits_{n \to \infty} \frac{\ln n}{n} = 0\).

A case where \(l=1\) and the series converges

Consider the series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\). We have \[\sqrt[n]{\frac{1}{n^2}} = \frac{1}{n^{\frac{2}{n}}}=e^{- \frac{2}{n} \ln n} \] Therefore \(\limsup\limits_{n \to \infty} \sqrt[n]{\frac{1}{n^2}} = 1\), while the series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\) is convergent as we have seen in the ratio test article.

Comparison of the ratio test and the root test

One can prove that if \(\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert\) exists, the equality \[
\limsup\limits_{n \to \infty} \sqrt[n]{\vert a_n \vert} = \lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert\] holds. Hence if the ratio test is conclusive, so is the root test. However the root test can succeed while the ratio test fails as shown by following example:
\[a_n=\begin{cases}
\frac{1}{2^n} & \text{if } n \text{ is odd}\\
\frac{1}{2^{n-2}} & \text{if } n \text{ is even}
\end{cases}\] for which \(\limsup\limits_{n \to \infty} \sqrt[n]{\vert a_n \vert}=\frac{1}{2}\) while
\[\frac{a_{n+1}}{a_n}=\begin{cases}
2 & \text{if } n \text{ is odd}\\
\frac{1}{8} & \text{if } n \text{ is even}
\end{cases}\] In that case the root test allows to conclude that the series converges and the ratio test is inconclusive as \(\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert\) doesn’t exist.