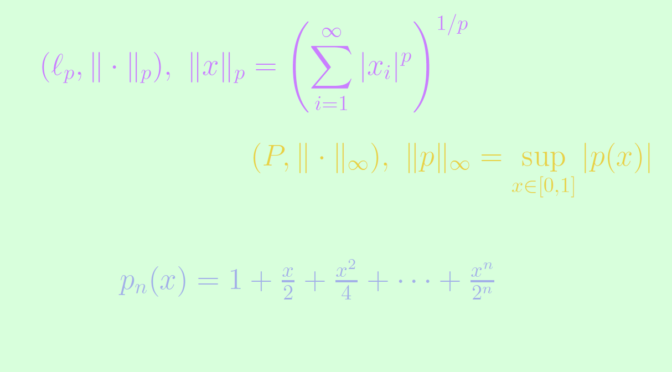Topology

A non complete normed vector space

Leave a comment

Consider a real normed vector space \(V\). \(V\) is called complete if every Cauchy sequence in \(V\) converges in \(V\). A complete normed vector space is also called a Banach space.

A finite dimensional vector space is complete. This is a consequence of a theorem stating that all norms on finite dimensional vector spaces are equivalent.

There are many examples of Banach spaces with infinite dimension like \((\ell_p, \Vert \cdot \Vert_p)\) the space of real sequences endowed with the norm \(\displaystyle \Vert x \Vert_p = \left( \sum_{i=1}^\infty \vert x_i \vert^p \right)^{1/p}\) for \(p \ge 1\), the space \((C(X), \Vert \cdot \Vert)\) of real continuous functions on a compact Hausdorff space \(X\) endowed with the norm \(\displaystyle \Vert f \Vert = \sup\limits_{x \in X} \vert f(x) \vert\) or the Lebesgue space \((L^1(\mathbb R), \Vert \cdot \Vert_1)\) of Lebesgue real integrable functions endowed with the norm \(\displaystyle \Vert f \Vert = \int_{\mathbb R} \vert f(x) \vert \ dx\).

Let’s give an example of a non complete normed vector space. Let \((P, \Vert \cdot \Vert_\infty)\) be the normed vector space of real polynomials endowed with the norm \(\displaystyle \Vert p \Vert_\infty = \sup\limits_{x \in [0,1]} \vert p(x) \vert\). Consider the sequence of polynomials \((p_n)\) defined by
\[p_n(x) = 1 + \frac{x}{2} + \frac{x^2}{4} + \cdots + \frac{x^n}{2^n} = \sum_{k=0}^{n} \frac{x^k}{2^k}.\] For \(m < n \) and \(x \in [0,1]\), we have \[\vert p_n(x) - p_m(x) \vert = \left\vert \sum_{i=m+1}^n \frac{x^i}{2^i} \right\vert \le \sum_{i=m+1}^n \frac{1}{2^i} \le \frac{1}{2^m}\] which proves that \((p_n)\) is a Cauchy sequence. Also for \(x \in [0,1]\) \[ \lim\limits_{n \to \infty} p_n(x) = p(x) \text{ where } p(x) = \frac{1}{1 - \frac{x}{2}}.\] As uniform converge implies pointwise convergence, if \((p_n)\) was convergent in \(P\), it would be towards \(p\). But \(p\) is not a polynomial function as none of its \(n\)th-derivative always vanishes. Hence \((p_n)\) is a Cauchy sequence that doesn't converge in \((P, \Vert \cdot \Vert_\infty)\), proving as desired that this normed vector space is not complete. More generally, a normed vector space with countable dimension is never complete. This can be proven using Baire category theorem which states that a non-empty complete metric space is not the countable union of nowhere-dense closed sets.

Analysis

Uniform continuous function but not Lipschitz continuous

Leave a comment

Consider the function \[
\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & [0,1] \\
& x & \longmapsto & \sqrt{x} \end{array}\]

\(f\) is continuous on the compact interval \([0,1]\). Hence \(f\) is uniform continuous on that interval according to Heine-Cantor theorem. For a direct proof, one can verify that for \(\epsilon > 0\), one have \(\vert \sqrt{x} – \sqrt{y} \vert \le \epsilon\) for \(\vert x – y \vert \le \epsilon^2\).

However \(f\) is not Lipschitz continuous. If \(f\) was Lipschitz continuous for a Lipschitz constant \(K > 0\), we would have \(\vert \sqrt{x} – \sqrt{y} \vert \le K \vert x – y \vert\) for all \(x,y \in [0,1]\). But we get a contradiction taking \(x=0\) and \(y=\frac{1}{4 K^2}\) as \[
\vert \sqrt{x} – \sqrt{y} \vert = \frac{1}{2 K} > \frac{1}{4 K} = K \vert x – y \vert\]

Algebra

A nonabelian \(p\)-group

Leave a comment

Consider a prime number \(p\) and a finite p-group \(G\), i.e. a group of order \(p^n\) with \(n \ge 1\).

If \(n=1\) the group \(G\) is cyclic hence abelian.

For \(n=2\), \(G\) is also abelian. This is a consequence of the fact that the center \(Z(G)\) of a \(p\)-group is non-trivial. Indeed if \(\vert Z(G) \vert =p^2\) then \(G=Z(G)\) is abelian. We can’t have \(\vert Z(G) \vert =p\). If that would be the case, the order of \(H=G / Z(G) \) would be equal to \(p\) and \(H\) would be cyclic, generated by an element \(h\). For any two elements \(g_1,g_2 \in G\), we would be able to write \(g_1=h^{n_1} z_1\) and \(g_2=h^{n_1} z_1\) with \(z_1,z_2 \in Z(G)\). Hence \[
g_1 g_2 = h^{n_1} z_1 h^{n_2} z_2=h^{n_1 + n_2} z_1 z_2= h^{n_2} z_2 h^{n_1} z_1=g_2 g_1,\] proving that \(g_1,g_2\) commutes in contradiction with \(\vert Z(G) \vert < \vert G \vert\). However, all \(p\)-groups are not abelian. For example the unitriangular matrix group \[
U(3,\mathbb Z_p) = \left\{
\begin{pmatrix}
1 & a & b\\
0 & 1 & c\\
0 & 0 & 1\end{pmatrix} \ | \ a,b ,c \in \mathbb Z_p \right\}\] is a \(p\)-group of order \(p^3\). Its center \(Z(U(3,\mathbb Z_p))\) is \[
Z(U(3,\mathbb Z_p)) = \left\{
\begin{pmatrix}
1 & 0 & b\\
0 & 1 & 0\\
0 & 0 & 1\end{pmatrix} \ | \ b \in \mathbb Z_p \right\},\] which is of order \(p\). Therefore \(U(3,\mathbb Z_p)\) is not abelian.

Analysis

Raabe-Duhamel’s test

Leave a comment

The Raabe-Duhamel’s test (also named Raabe’s test) is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number. The Raabe-Duhamel’s test was developed by Swiss mathematician Joseph Ludwig Raabe.

It states that if:

\[\displaystyle \lim _{n\to \infty }\left\vert{\frac {a_{n}}{a_{n+1}}}\right\vert=1 \text{ and } \lim _{{n\to \infty }} n \left(\left\vert{\frac {a_{n}}{a_{{n+1}}}}\right\vert-1 \right)=R,\]
then the series will be absolutely convergent if \(R > 1\) and divergent if \(R < 1\). First one can notice that Raabe-Duhamel's test maybe conclusive in cases where ratio test isn't. For instance, consider a real \(\alpha\) and the series \(u_n=\frac{1}{n^\alpha}\). We have \[ \lim _{n\to \infty } \frac{u_{n+1}}{u_n} = \lim _{n\to \infty } \left(\frac{n}{n+1} \right)^\alpha = 1\] and therefore the ratio test is inconclusive. However \[ \frac{u_n}{u_{n+1}} = \left(\frac{n+1}{n} \right)^\alpha = 1 + \frac{\alpha}{n} + o \left(\frac{1}{n}\right)\] for \(n\) around \(\infty\) and \[ \lim _{{n\to \infty }} n \left(\frac {u_{n}}{u_{{n+1}}}-1 \right)=\alpha.\] Raabe-Duhamel's test allows to conclude that the series \(\sum u_n\) diverges for \(\alpha <1\) and converges for \(\alpha > 1\) as well known.

When \(R=1\) in the Raabe’s test, the series can be convergent or divergent. For example, the series above \(u_n=\frac{1}{n^\alpha}\) with \(\alpha=1\) is the harmonic series which is divergent.

On the other hand, the series \(v_n=\frac{1}{n \log^2 n}\) is convergent as can be proved using the integral test. Namely \[
0 \le \frac{1}{n \log^2 n} \le \int_{n-1}^n \frac{dt}{t \log^2 t} \text{ for } n \ge 3\] and \[
\int_2^\infty \frac{dt}{t \log^2 t} = \left[-\frac{1}{\log t} \right]_2^\infty = \frac{1}{\log 2}\] is convergent, while \[
\frac{v_n}{v_{n+1}} = 1 + \frac{1}{n} +\frac{2}{n \log n} + o \left(\frac{1}{n \log n}\right)\] for \(n\) around \(\infty\) and therefore \(R=1\) in the Raabe-Duhamel’s test.

Algebra

Subset of elements of finite order of a group

Leave a comment

Consider a group \(G\) and have a look at the question: is the subset \(S\) of elements of finite order a subgroup of \(G\)?

The answer is positive when any two elements of \(S\) commute. For the proof, consider \(x,y \in S\) of order \(m,n\) respectively. Then \[
\left(xy\right)^{mn} = x^{mn} y^{mn} = (x^m)^n (y^n)^m = e\] where \(e\) is the identity element. Hence \(xy\) is of finite order (less or equal to \(mn\)) and belong to \(S\).

Example of a non abelian group

In that cas, \(S\) might not be subgroup of \(G\). Let’s take for \(G\) the general linear group over \(\mathbb Q\) (the set of rational numbers) of \(2 \times 2\) invertible matrices named \(\text{GL}_2(\mathbb Q)\). The matrices \[
A = \begin{pmatrix}0&1\\1&0\end{pmatrix},\ B=\begin{pmatrix}0 & 2\\\frac{1}{2}& 0\end{pmatrix}\] are of order \(2\). They don’t commute as \[
AB = \begin{pmatrix}\frac{1}{2}&0\\0&2\end{pmatrix} \neq \begin{pmatrix}2&0\\0&\frac{1}{2}\end{pmatrix}=BA.\] Finally, \(AB\) is of infinite order and therefore doesn’t belong to \(S\) proving that \(S\) is not a subgroup of \(G\).

Analysis

Counterexamples around Cauchy condensation test

1 Comment

According to Cauchy condensation test: for a non-negative, non-increasing sequence \((u_n)_{n \in \mathbb N}\) of real numbers, the series \(\sum_{n \in \mathbb N} u_n\) converges if and only if the condensed series \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) converges.

The test doesn’t hold for any non-negative sequence. Let’s have a look at counterexamples.

A sequence such that \(\sum_{n \in \mathbb N} u_n\) converges and \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges

Consider the sequence \[
u_n=\begin{cases}
\frac{1}{n} & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
0 & \text{ else} \end{cases}\] For \(n \in \mathbb N\) we have \[
0 \le \sum_{k = 1}^n u_k \le \sum_{k = 1}^{2^n} u_k = \sum_{k = 1}^{n} \frac{1}{2^k} < 1,\] therefore \(\sum_{n \in \mathbb N} u_n\) converges as its partial sums are positive and bounded above. However \[\sum_{k=1}^n 2^k u_{2^k} = \sum_{k=1}^n 1 = n,\] so \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges.

A sequence such that \(\sum_{n \in \mathbb N} v_n\) diverges and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges

Consider the sequence \[
v_n=\begin{cases}
0 & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
\frac{1}{n} & \text{ else} \end{cases}\] We have \[
\sum_{k = 1}^{2^n} v_k = \sum_{k = 1}^{2^n} \frac{1}{k} – \sum_{k = 1}^{n} \frac{1}{2^k} > \sum_{k = 1}^{2^n} \frac{1}{k} -1\] which proves that the series \(\sum_{n \in \mathbb N} v_n\) diverges as the harmonic series is divergent. However for \(n \in \mathbb N\), \(2^n v_{2^n} = 0 \) and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges.

Analysis

Counterexamples around the Cauchy product of real series

Leave a comment

Let \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) be two series of real numbers. The Cauchy product \(\sum_{n = 0}^\infty c_n\) is the series defined by \[
c_n = \sum_{k=0}^n a_k b_{n-k}\] According to the theorem of Mertens, if \(\sum_{n = 0}^\infty a_n\) converges to \(A\), \(\sum_{n = 0}^\infty b_n\) converges to \(B\) and at least one of the two series is absolutely convergent, their Cauchy product converges to \(AB\). This can be summarized by the equality \[
\left( \sum_{n = 0}^\infty a_n \right) \left( \sum_{n = 0}^\infty b_n \right) = \sum_{n = 0}^\infty c_n\]

The assumption stating that at least one of the two series converges absolutely cannot be dropped as shown by the example \[
\sum_{n = 0}^\infty a_n = \sum_{n = 0}^\infty b_n = \sum_{n = 0}^\infty \frac{(-1)^n}{\sqrt{n+1}}\] Those series converge according to Leibniz test, as the sequence \((1/\sqrt{n+1})\) decreases monotonically to zero. However, the Cauchy product is defined by \[
c_n=\sum_{k=0}^n \frac{(-1)^k}{\sqrt{k+1}} \cdot \frac{(-1)^{n-k}}{\sqrt{n-k+1}} = (-1)^n \sum_{k=0}^n \frac{1}{\sqrt{(k+1)(n-k+1)}}\] As we have \(1 \le k+ 1 \le n+1\) and \(1 \le n-k+ 1 \le n+1\) for \(k = 0 \dots n\), we get \(\frac{1}{\sqrt{(k+1)(n-k+1)}} \ge \frac{1}{n+1}\) and therefore \(\vert c_n \vert \ge 1\) proving that the Cauchy product of \(\sum_{n = 0}^\infty a_n\) and \(\sum_{n = 0}^\infty b_n\) diverges.

The Cauchy product may also converge while the initial series both diverge. Let’s consider \[
\begin{cases}
(a_n) = (2, 2, 2^2, \dots, 2^n, \dots)\\
(b_n) = (-1, 1, 1, 1, \dots)
\end{cases}\] The series \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) diverge. Their Cauchy product is the series defined by \[
c_n=\begin{cases}
-2 & \text{ for } n=0\\
0 & \text{ for } n>0
\end{cases}\] which is convergent.

Analysis

A linear differential equation with no solution to an initial value problem

Leave a comment


Consider a first order linear differential equation \[
y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B\) are real continuous functions defined on a non-empty real interval \(I\). According to Picard-Lindelöf theorem, the initial value problem \[
\begin{cases}
y^\prime(x) = A(x)y(x) + B(x)\\
y(x_0) = y_0, \ x_0 \in I
\end{cases}\] has a unique solution defined on \(I\).

However, a linear differential equation \[
c(x)y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B, c\) are real continuous functions might not have a solution to an initial value problem. Let’s have a look at the equation \[
x y^\prime(x) = y(x) \tag{E}\label{eq:IVP}\] for \(x \in \mathbb R\). The equation is linear.

For \(x \in (-\infty,0)\) a solution to \eqref{eq:IVP} is a solution of the explicit differential linear equation \[
y^\prime(x) = \frac{y(x)}x\] hence can be written \(y(x) = \lambda_-x\) with \(\lambda_- \in \mathbb R\). Similarly, a solution to \eqref{eq:IVP} on the interval \((0,\infty)\) is of the form \(y(x) = \lambda_+ x\) with \(\lambda_+ \in \mathbb R\).

A global solution to \eqref{eq:IVP}, i.e. defined on the whole real line is differentiable at \(0\) hence the equation \[
\lambda_- = y_-^\prime(0)=y_+^\prime(0) = \lambda_+\] which means that \(y(x) = \lambda x\) where \(\lambda=\lambda_-=\lambda_+\).

In particular all solutions defined on \(\mathbb R\) are such that \(y(0)=0\). Therefore the initial value problem \[
\begin{cases}
x y^\prime(x) = y(x)\\
y(0)=1
\end{cases}\] has no solution.

Algebra

Field not algebraic over an intersection but algebraic over each initial field

Leave a comment

Let’s describe an example of a field \(K\) which is of degree \(2\) over two distinct subfields \(M\) and \(N\) respectively, but not algebraic over \(M \cap N\).

Let \(K=F(x)\) be the rational function field over a field \(F\) of characteristic \(0\), \(M=F(x^2)\) and \(N=F(x^2+x)\). I claim that those fields provide the example we’re looking for.

\(K\) is of degree \(2\) over \(M\) and \(N\)

The polynomial \(\mu_M(t)=t^2-x^2\) belongs to \(M[t]\) and \(x \in K\) is a root of \(\mu_M\). Also, \(\mu_M\) is irreducible over \(M=F(x^2)\). If that wasn’t the case, \(\mu_M\) would have a root in \(F(x^2)\) and there would exist two polynomials \(p,q \in F[t]\) such that \[
p^2(x^2) = x^2 q^2(x^2)\] which cannot be, as can be seen considering the degrees of the polynomials of left and right hand sides. This proves that \([K:M]=2\). Considering the polynomial \(\mu_N(t)=t^2-t-(x^2+x)\), one can prove that we also have \([K:N]=2\).

We have \(M \cap N=F\)

The mapping \(\sigma_M : x \mapsto -x\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(M\) are fixed under \(\sigma_M\). Similarly, the mapping \(\sigma_N : x \mapsto -x-1\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(N\) are fixed under \(\sigma_N\). Also \[
(\sigma_N\circ\sigma_M)(x)=\sigma_N(\sigma_M(x))=\sigma_N(-x)=-(-x-1)=x+1.\] An element \(z=p(x)/q(x) \in M \cap N\) where \(p(x),q(x)\) are coprime polynomials of \(K=F(x)\) is fixed under \(\sigma_M \circ \sigma_N\). Therefore following equality holds \[
\frac{p(x)}{q(x)}=z=(\sigma_2\circ\sigma_1)(z)=\frac{p(x+1)}{q(x+1)},\] which is equivalent to \[
p(x)q(x+1)=p(x+1)q(x).\] By induction, we get for \(n \in \mathbb Z\) \[
p(x)q(x+n)=p(x+n)q(x).\] Assume \(p(x)\) is not a constant polynomial. Then it has a root \(\alpha\) in some finite extension \(E\) of \(F\). As \(p(x),q(x)\) are coprime polynomials, \(q(\alpha) \neq 0\). Consequently \(p(\alpha+n)=0\) for all \(n \in \mathbb Z\) and the elements \(\alpha +n\) are all distinct as the characteristic of \(F\) is supposed to be non zero. This implies that \(p(x)\) is the zero polynomial, in contradiction with our assumption. Therefore \(p(x)\) is a constant polynomial and \(q(x)\) also according to a similar proof. Hence \(z\) is constant as was supposed to be proven.

Finally, \(K=F(x)\) is not algebraic over \(F=M \cap N\) as \((1,x, x^2, \dots, x^n, \dots)\) is independent over the field \(F\) which concludes our claims on \(K, M\) and \(N\).

Analysis

Pointwise convergence not uniform on any interval

Leave a comment

We provide in this article an example of a pointwise convergent sequence of real functions that doesn’t converge uniformly on any interval.

Let’s consider a sequence \((a_p)_{p \in \mathbb N}\) enumerating the set \(\mathbb Q\) of rational numbers. Such a sequence exists as \(\mathbb Q\) is countable.

Now let \((g_n)_{n \in \mathbb N}\) be the sequence of real functions defined on \(\mathbb R\) by \[
g_n(x) = \sum_{p=1}^{\infty} \frac{1}{2^p} f_n(x-a_p)\] where \(f_n : x \mapsto \frac{n^2 x^2}{1+n^4 x^4}\) for \(n \in \mathbb N\).

\(f_n\) main properties

\(f_n\) is a rational function whose denominator doesn’t vanish. Hence \(f_n\) is indefinitely differentiable. As \(f_n\) is an even function, we can study it only on \([0,\infty)\).

We have \[
f_n^\prime(x)= 2n^2x \frac{1-n^4x^4}{(1+n^4 x^4)^2}.\] \(f_n^\prime\) vanishes at zero (like \(f_n\)) is positive on \((0,\frac{1}{n})\), vanishes at \(\frac{1}{n}\) and is negative on \((\frac{1}{n},\infty)\). Hence \(f_n\) has a maximum at \(\frac{1}{n}\) with \(f_n(\frac{1}{n}) = \frac{1}{2}\) and \(0 \le f_n(x) \le \frac{1}{2}\) for all \(x \in \mathbb R\).

Also for \(x \neq 0\) \[
0 \le f_n(x) =\frac{n^2 x^2}{1+n^4 x^4} \le \frac{n^2 x^2}{n^4 x^4} = \frac{1}{n^2 x^2}\] consequently \[
0 \le f_n(x) \le \frac{1}{n} \text{ for } x \ge \frac{1}{\sqrt{n}}.\]

\((g_n)\) converges pointwise to zero

First, one can notice that \(g_n\) is well defined. For \(x \in \mathbb R\) and \(p \in \mathbb N\) we have \(0 \le \frac{1}{2^p} f_n(x-a_p) \le \frac{1}{2^p} \cdot\ \frac{1}{2}=\frac{1}{2^{p+1}}\) according to previous paragraph. Therefore the series of functions \(\sum \frac{1}{2^p} f_n(x-a_p)\) is normally convergent. \(g_n\) is also continuous as for all \(p \in \mathbb N\) \(x \mapsto \frac{1}{2^p} f_n(x-a_p)\) is continuous. Continue reading Pointwise convergence not uniform on any interval →

Mathematical exceptions to the rules or intuition