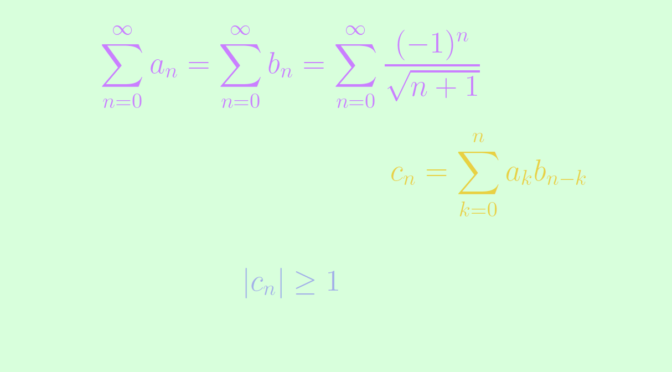Let \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) be two series of real numbers. The Cauchy product \(\sum_{n = 0}^\infty c_n\) is the series defined by \[
c_n = \sum_{k=0}^n a_k b_{n-k}\] According to the theorem of Mertens, if \(\sum_{n = 0}^\infty a_n\) converges to \(A\), \(\sum_{n = 0}^\infty b_n\) converges to \(B\) and at least one of the two series is absolutely convergent, their Cauchy product converges to \(AB\). This can be summarized by the equality \[
\left( \sum_{n = 0}^\infty a_n \right) \left( \sum_{n = 0}^\infty b_n \right) = \sum_{n = 0}^\infty c_n\]

The assumption stating that at least one of the two series converges absolutely cannot be dropped as shown by the example \[
\sum_{n = 0}^\infty a_n = \sum_{n = 0}^\infty b_n = \sum_{n = 0}^\infty \frac{(-1)^n}{\sqrt{n+1}}\] Those series converge according to Leibniz test, as the sequence \((1/\sqrt{n+1})\) decreases monotonically to zero. However, the Cauchy product is defined by \[
c_n=\sum_{k=0}^n \frac{(-1)^k}{\sqrt{k+1}} \cdot \frac{(-1)^{n-k}}{\sqrt{n-k+1}} = (-1)^n \sum_{k=0}^n \frac{1}{\sqrt{(k+1)(n-k+1)}}\] As we have \(1 \le k+ 1 \le n+1\) and \(1 \le n-k+ 1 \le n+1\) for \(k = 0 \dots n\), we get \(\frac{1}{\sqrt{(k+1)(n-k+1)}} \ge \frac{1}{n+1}\) and therefore \(\vert c_n \vert \ge 1\) proving that the Cauchy product of \(\sum_{n = 0}^\infty a_n\) and \(\sum_{n = 0}^\infty b_n\) diverges.

The Cauchy product may also converge while the initial series both diverge. Let’s consider \[
\begin{cases}
(a_n) = (2, 2, 2^2, \dots, 2^n, \dots)\\
(b_n) = (-1, 1, 1, 1, \dots)
\end{cases}\] The series \(\sum_{n = 0}^\infty a_n, \sum_{n = 0}^\infty b_n\) diverge. Their Cauchy product is the series defined by \[
c_n=\begin{cases}
-2 & \text{ for } n=0\\
0 & \text{ for } n>0
\end{cases}\] which is convergent.