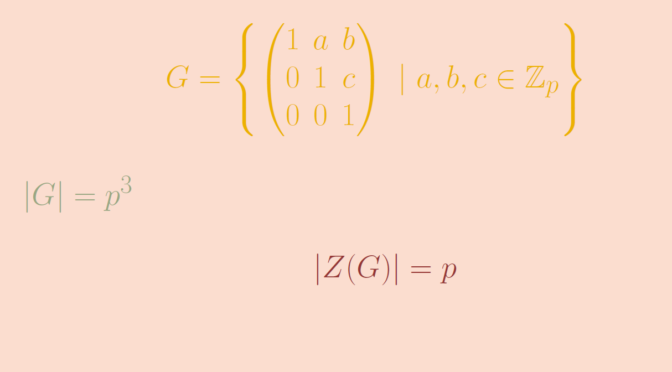Consider a prime number $p$ and a finite p-group $G$, i.e. a group of order $p^n$ with $n \ge 1$.

If $n=1$ the group $G$ is cyclic hence abelian.

For $n=2$, $G$ is also abelian. This is a consequence of the fact that the center $Z(G)$ of a $p$-group is non-trivial. Indeed if $\vert Z(G) \vert =p^2$ then $G=Z(G)$ is abelian. We can’t have $\vert Z(G) \vert =p$. If that would be the case, the order of $H=G / Z(G)$ would be equal to $p$ and $H$ would be cyclic, generated by an element $h$. For any two elements $g_1,g_2 \in G$, we would be able to write $g_1=h^{n_1} z_1$ and $g_2=h^{n_1} z_1$ with $z_1,z_2 \in Z(G)$. Hence $$g_1 g_2 = h^{n_1} z_1 h^{n_2} z_2=h^{n_1 + n_2} z_1 z_2= h^{n_2} z_2 h^{n_1} z_1=g_2 g_1,$$ proving that $g_1,g_2$ commutes in contradiction with $\vert Z(G) \vert < \vert G \vert$. However, all $p$-groups are not abelian. For example the unitriangular matrix group $$U(3,\mathbb Z_p) = \left\{ \begin{pmatrix} 1 & a & b\\ 0 & 1 & c\\ 0 & 0 & 1\end{pmatrix} \ | \ a,b ,c \in \mathbb Z_p \right\}$$ is a $p$-group of order $p^3$. Its center $Z(U(3,\mathbb Z_p))$ is $$Z(U(3,\mathbb Z_p)) = \left\{ \begin{pmatrix} 1 & 0 & b\\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix} \ | \ b \in \mathbb Z_p \right\},$$ which is of order $p$. Therefore $U(3,\mathbb Z_p)$ is not abelian.