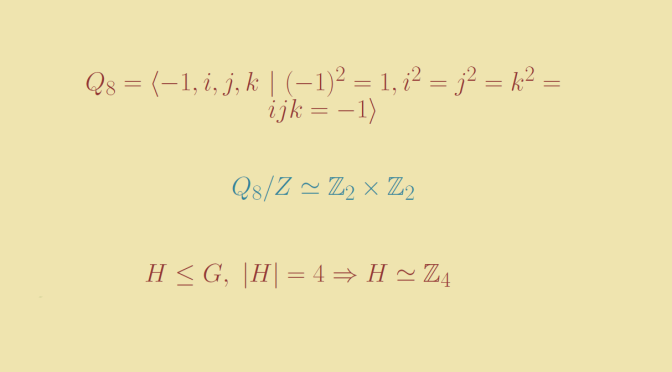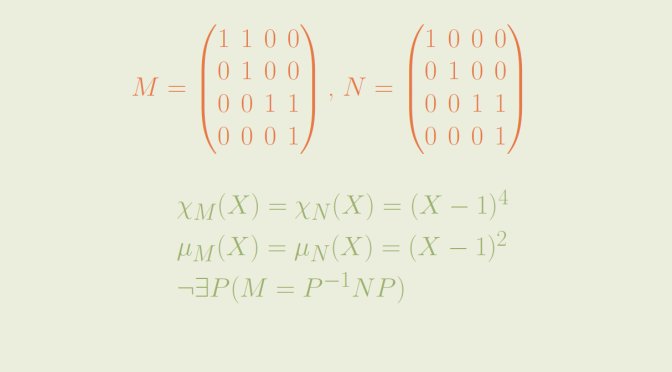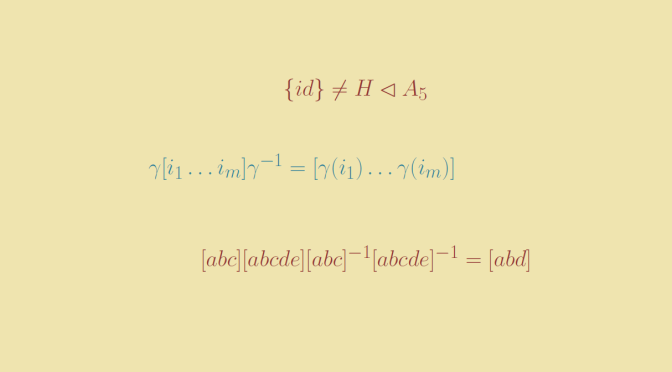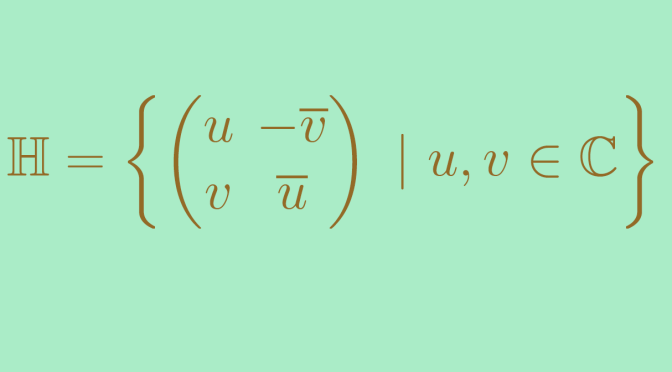Category Archives: Algebra

Algebra

Is the quotient group of a finite group always isomorphic to a subgroup?

Leave a comment

Given a normal subgroup \(H\) of a finite group \(G\), is \(G/H\) always isomorphic to a subgroup \(K \le G\)?

The case of an abelian group

According to the fundamental theorem of finite abelian groups, every finite abelian group \(G\) can be expressed as the direct sum of cyclic subgroups of prime-power order: \[G \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i}}\] where \(p_1, \dots , p_u\) are primes and \(\alpha_1, \dots , \alpha_u\) non zero integers.

If \(H \le G\) we have \[H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\beta_i}}\] with \(0 \le \beta_1 \le \alpha_1, \dots, 0 \le \beta_u \le \alpha_u\). Then \[G/H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i-\beta_i}}\] which is a subgroup of \(G\).

If \(G\) is not abelian, then \(G/H\) might not be isomorphic to a subgroup of \(G\). Continue reading Is the quotient group of a finite group always isomorphic to a subgroup? →

Algebra

Two non similar matrices having same minimal and characteristic polynomials

Leave a comment

Consider a square matrix \(A\) of dimension \(n \ge 1\) over a field \(\mathbb F\), i.e. \(A \in \mathcal M_n(\mathbb F)\). Results discuss below are true for any field \(\mathbb F\), in particular for \(\mathbb F = \mathbb R\) or \(\mathbb F = \mathbb C\).

A polynomial \(P \in \mathbb F[X]\) is called a vanishing polynomial for \(A\) if \(P(A) = 0\). If the matrix \(B\) is similar to \(B\) (which means that \(B=Q^{-1} A Q\) for some invertible matrix \(Q\)), and the polynomial \(P\) vanishes at \(A\) then \(P\) also vanishes at \(B\). This is easy to prove as we have \(P(B)=P(Q^{-1} A Q)=Q^{-1} P(A) Q\).

In particular, two similar matrices have the same minimal and characteristic polynomials.

Is the converse true? Are two matrices having the same minimal and characteristic polynomials similar? Continue reading Two non similar matrices having same minimal and characteristic polynomials →

Algebra

A simple group whose order is not a prime

Leave a comment

Consider a finite group \(G\) whose order (number of elements) is a prime number. It is well known that \(G\) is cyclic and simple. Which means that \(G\) has no non trivial normal subgroup.

Is the converse true, i.e. are the cyclic groups with prime orders the only simple groups? The answer is negative. We prove here that for \(n \ge 5\) the alternating group \(A_n\) is simple. In particular \(A_5\) whose order is equal to \(60\) is simple. Continue reading A simple group whose order is not a prime →

Algebra

The skew field of Hamilton’s quaternions

Leave a comment

We give here an example of a division ring which is not commutative. According to Wedderburn theorem every finite division ring is commutative. So we must turn to infinite division rings to find a non-commutative one, i.e. a skew field.

Let’s introduce the skew field of the Hamilton’s quaternions \[\mathbb H = \left\{\begin{pmatrix}
u & -\overline{v} \\
v & \overline{u}
\end{pmatrix} \ | \ u,v \in \mathbb C\right\}\] Continue reading The skew field of Hamilton’s quaternions →

Algebra

An infinite group whose proper subgroups are all finite

Leave a comment

We study some properties of the Prüfer \(p\)-group \(\mathbb{Z}_{p^\infty}\) for a prime number \(p\). The Prüfer \(p\)-group may be identified with the subgroup of the circle group, consisting of all \(p^n\)-th roots of unity as \(n\) ranges over all non-negative integers:
\[\mathbb{Z}_{p^\infty}=\bigcup_{k=0}^\infty \mathbb{Z}_{p^k} \text{ where } \mathbb{Z}_{p^k}= \{e^{\frac{2 i \pi m}{p^k}} \ | \ 0 \le m \le p^k-1\}\]

\(\mathbb{Z}_{p^\infty}\) is a group

First, let’s notice that for \(0 \le m \le n\) integers we have \(\mathbb{Z}_{p^m} \subseteq \mathbb{Z}_{p^n}\) as \(p^m | p^n\). Also for \(m \ge 0\) \(\mathbb{Z}_{p^m}\) is a subgroup of the circle group. We also notice that all elements of \(\mathbb{Z}_{p^\infty}\) have finite orders which are powers of \(p\). Continue reading An infinite group whose proper subgroups are all finite →

Algebra

The set of all commutators in a group need not be a subgroup

Leave a comment

I here provide a simple example of a group whose set of commutators is not a subgroup. The counterexample is due to P.J. Cassidy (1979).

Description of the group \(G\)

Let \(k[x,y]\) denote the ring of all polynomials in two variables over a field \(k\), and let \(k[x]\) and \(k[y]\) denote the subrings of all polynomials in \(x\) and in \(y\) respectively. \(G\) is the set of all upper unitriangular matrices of the form
\[A=\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)\] where \(f(x) \in k[x]\), \(g(y) \in k[y]\), and \(h(x,y) \in k[x,y]\). The matrix \(A\) will also be denoted \((f,g,h)\).
Let’s verify that \(G\) is a group. The products of two elements \((f,g,h)\) and \((f^\prime,g^\prime,h^\prime)\) is
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc}
1 & f^\prime(x) & h^\prime(x,y) \\
0 & 1 & g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\]
\[=\left(\begin{array}{ccc}
1 & f(x)+f^\prime(x) & h(x,y)+h^\prime(x,y)+f(x)g^\prime(y) \\
0 & 1 & g(y)+g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\] which is an element of \(G\). We also have:
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)^{-1} =
\left(\begin{array}{ccc}
1 & -f(x) & f(x)g(y) – h(x,y) \\
0 & 1 & -g(y) \\
0 & 0 & 1 \end{array}\right)\] proving that the inverse of an element of \(G\) is also an element of \(G\). Continue reading The set of all commutators in a group need not be a subgroup →

Algebra

Generating the symmetric group with a transposition and a maximal length cycle

Leave a comment

Can the symmetric group \(\mathcal{S}_n\) be generated by any transposition and any \(n\)-cycle for \(n \ge 2\) integer? is the question we deal with.

We first recall some terminology:

Symmetric group
The symmetric group \(\mathcal{S}_n\) on a finite set of \(n\) symbols is the group whose elements are all the permutations of the \(n\) symbols. We’ll denote by \(\{1,\dots,n\}\) those \(n\) symbols.
Cycle
A cycle of length \(k\) (with \(k \ge 2\)) is a cyclic permutation \(\sigma\) for which there exists an element \(i \in \{1,\dots,n\}\) such that \(i, \sigma(i), \sigma^2(i), \dots, \sigma^k(i)=i\) are the only elements moved by \(\sigma\). We’ll denote the cycle \(\sigma\) by \((s_0 \ s_1 \dots \ s_{k-1})\) where \(s_0=i, s_1=\sigma(i),\dots,s_{k-1}=\sigma^{k-1}(i)\).
Transposition
A transposition is a cycle of length \(2\). We denote below the transposition of elements \(a \neq b\) by \((a \ b)\) or \(\tau_{a,b}\).

Continue reading Generating the symmetric group with a transposition and a maximal length cycle →

Algebra

Two subgroups whose product is not a subgroup

Leave a comment

In this article, we consider a group \(G\) and two subgroups \(H\) and \(K\). Let \(HK=\{hk \text{ | } h \in H, k \in K\}\).

\(HK\) is a subgroup of \(G\) if and only if \(HK=KH\). For the proof we first notice that if \(HK\) is a subgroup of \(G\) then it’s closed under inverses so \(HK = (HK)^{-1} = K^{-1}H^{-1} = KH\). Conversely if \(HK = KH\) then take \(hk\), \(h^\prime k^\prime \in HK\). Then \((hk)(h^\prime k^\prime)^{-1} = hk(k^\prime)^{-1}(h^\prime)^{-1}\). Since \(HK = KH\) we can rewrite \(k(k^\prime)^{-1}(h^\prime)^{-1}\) as \(h^{\prime \prime}k^{\prime \prime}\) for some new \(h^{\prime \prime} \in H\), \(k^{\prime \prime} \in K\). So \((hk)(h^\prime k^\prime)^{-1}=hh^{\prime \prime}k^{\prime \prime}\) which is in \(HK\). This verifies that \(HK\) is a subgroup. Continue reading Two subgroups whose product is not a subgroup →

Algebra

One matrix having several interesting properties

Leave a comment

We consider a vector space \(V\) of dimension \(2\) over a field \(\mathbb{K}\). The matrix:
\[A=\left( \begin{array}{cc}
0 & 1 \\
0 & 0 \end{array} \right)\] has several wonderful properties!

Only zero as eigenvalue, but minimal polynomial of degree \(2\)

Zero is the only eigenvalue. The corresponding characteristic space is \(\mathbb{K} . e_1\) where \((e_1,e_2)\) is the standard basis. The minimal polynomial of \(A\) is \(\mu_A(X)=X^2\). Continue reading One matrix having several interesting properties →