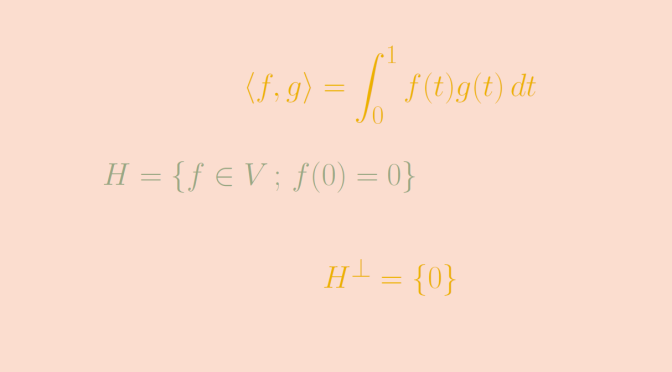Category Archives: Algebra

Algebra

A simple ring which is not a division ring

Leave a comment

Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.

We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.

Let’s prove first following lemma. Continue reading A simple ring which is not a division ring →

Algebra

Unique factorization domain that is not a Principal ideal domain

Leave a comment

In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.

We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.

The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.

Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).

But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).

Algebra

A proper subspace without an orthogonal complement

Leave a comment

We consider an inner product space \(V\) over the field of real numbers \(\mathbb R\). The inner product is denoted by \(\langle \cdot , \cdot \rangle\).

When \(V\) is a finite dimensional space, every proper subspace \(F \subset V\) has an orthogonal complement \(F^\perp\) with \(V = F \oplus F^\perp\). This is no more true for infinite dimensional spaces and we present here an example.

Consider the space \(V=\mathcal C([0,1],\mathbb R)\) of the continuous real functions defined on the segment \([0,1]\). The bilinear map
\[\begin{array}{l|rcl}
\langle \cdot , \cdot \rangle : & V \times V & \longrightarrow & \mathbb R \\
& (f,g) & \longmapsto & \langle f , g \rangle = \displaystyle \int_0^1 f(t)g(t) \, dt \end{array}
\] is an inner product on \(V\).

Let’s consider the proper subspace \(H = \{f \in V \, ; \, f(0)=0\}\). \(H\) is an hyperplane of \(V\) as \(H\) is the kernel of the linear form \(\varphi : f \mapsto f(0)\) defined on \(V\). \(H\) is a proper subspace as \(\varphi\) is not always vanishing. Let’s prove that \(H^\perp = \{0\}\).

Take \(g \in H^\perp\). By definition of \(H^\perp\) we have \(\int_0^1 f(t) g(t) \, dt = 0\) for all \(f \in H\). In particular the function \(h : t \mapsto t g(t)\) belongs to \(H\). Hence
\[0 = \langle h , g \rangle = \displaystyle \int_0^1 t g(t)g(t) \, dt\] The map \(t \mapsto t g^2(t)\) is continuous, non-negative on \([0,1]\) and its integral on this segment vanishes. Hence \(t g^2(t)\) is always vanishing on \([0,1]\), and \(g\) is always vanishing on \((0,1]\). As \(g\) is continuous, we finally get that \(g = 0\).

\(H\) doesn’t have an orthogonal complement.

Moreover we have
\[(H^\perp)^\perp = \{0\}^\perp = V \neq H\]

Algebra

Intersection and sum of vector subspaces

Leave a comment

Let’s consider a vector space \(E\) over a field \(K\). We’ll look at relations involving basic set operations and sum of subspaces. We denote by \(F, G\) and \(H\) subspaces of \(E\).

The relation \((F \cap G) + H \subset (F+H) \cap (G + H)\)

This relation holds. The proof is quite simple. For any \(x \in (F \cap G) + H\) there exists \(y \in F \cap G\) and \(h \in H\) such that \(x=y+h\). As \(y \in F\), \(x \in F+H\) and by a similar argument \(x \in F+H\). Therefore \(x \in (F+H) \cap (G + H)\).

Is the inclusion \((F \cap G) + H \subset (F+H) \cap (G + H)\) always an equality? The answer is negative. Take for the space \(E\) the real 3 dimensional space \(\mathbb R^3\). And for the subspaces:

  • \(H\) the plane of equation \(z=0\),
  • \(F\) the line of equations \(y = 0, \, x=z\),
  • \(G\) the line of equations \(y = 0, \, x=-z\),

Continue reading Intersection and sum of vector subspaces →

Algebra

A non Archimedean ordered field

1 Comment

Let’s recall that an ordered field \(K\) is said to be Archimedean if for any \(a,b \in K\) such that \(0 \lt a \lt b\) it exists a natural number \(n\) such that \(na > b\).

The ordered fields \(\mathbb Q\) or \(\mathbb R\) are Archimedean. We introduce here the example of an ordered field which is not Archimedean. Let’s consider the field of rational functions
\[\mathbb R(x) = \left\{\frac{S(x)}{T(x)} \ | \ S, T \in \mathbb R[x] \right\}\] For \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) we can suppose that the polynomials have a constant polynomial greatest common divisor.

Now we define \(P\) as the set of elements \(f(x)=\frac{S(x)}{T(x)} \in \mathbb R(x)\) in which the leading coefficients of \(S\) and \(T\) have the same sign.

One can verify that the subset \(P \subset \mathbb R(x)\) satisfies following two conditions:

ORD 1
Given \(f(x) \in \mathbb R(x)\), we have either \(f(x) \in P\), or \(f(x)=0\), or \(-f(x) \in P\), and these three possibilities are mutually exclusive. In other words, \(\mathbb R(x)\) is the disjoint union of \(P\), \(\{0\}\) and \(-P\).
ORD 2
For \(f(x),g(x) \in P\), \(f(x)+g(x)\) and \(f(x)g(x)\) belong to \(P\).

This means that \(P\) is a positive cone of \(\mathbb R(x)\). Hence, \(\mathbb R(x)\) is ordered by the relation
\[f(x) > 0 \Leftrightarrow f(x) \in P.\]

Now let’s consider the rational fraction \(h(x)=\frac{x}{1} \in \mathbb R(x)\). \(h(x)\) is a positive element, i.e. belongs to \(P\) as \(h-1 = \frac{x-1}{1}\). For any \(n \in \mathbb N\), we have
\[h – n 1=\frac{x-n}{1} \in P\] as the leading coefficients of \(x-n\) and \(1\) are both equal to \(1\). Therefore, we have \(h \gt n 1\) for all \(n \in \mathbb N\), proving that \(\mathbb R(x)\) is not Archimedean.

Algebra

Infinite rings and fields with positive characteristic

Leave a comment

Familiar to us are infinite fields whose characteristic is equal to zero like \(\mathbb Z, \mathbb Q, \mathbb R\) or the field of constructible numbers.

We’re also familiar with rings having infinite number of elements and zero for characteristic like:

  • The rings of polynomials \(\mathbb Z[X], \mathbb Q[X], \mathbb R[X]\).
  • The rings of matrices \(\mathcal{M}_2(\mathbb R)\).
  • Or the ring of real continuous functions defined on \(\mathbb R\).

We also know rings or fields like integers modulo \(n\) (with \(n \ge 2\)) \(\mathbb Z_n\) or the finite field \(\mathbb F_q\) with \(q=p^r\) elements where \(p\) is a prime.

We provide below examples of infinite rings or fields with positive characteristic.

Infinite rings with positive characteristic

Consider the ring \(\mathbb Z_n[X]\) of polynomials in one variable \(X\) with coefficients in \(\mathbb Z_n\) for \(n \ge 2\) integer. It is an infinite ring since \(\mathbb X^m \in \mathbb{Z}_n[X]\) for all positive integers \(m\), and \(X^r \neq X^s\) for \(r \neq s\). But the characteristic of \(\mathbb Z_n[X]\) is clearly \(n\).

Another example is based on product of rings. If \(I\) is an index set and \((R_i)_{i \in I}\) a family of rings, one can define the product ring \(\displaystyle \prod_{i \in I} R_i\). The operations are defined the natural way with \((a_i)_{i \in I} + (b_i)_{i \in I} = (a_i+b_i)_{i \in I}\) and \((a_i)_{i \in I} \cdot (b_i)_{i \in I} = (a_i \cdot b_i)_{i \in I}\). Fixing \(n \ge 2\) integer and taking \(I = \mathbb N\), \(R_i = \mathbb Z_n\) for all \(i \in I\) we get the ring \(\displaystyle R = \prod_{k \in \mathbb N} \mathbb Z_n\). \(R\) multiplicative identity is the sequence with all terms equal to \(1\). The characteristic of \(R\) is \(n\) and \(R\) is obviously infinite. Continue reading Infinite rings and fields with positive characteristic →

Algebra

A ring whose characteristic is a prime having a zero divisor

Leave a comment

Consider a ring \(R\) whose characteristic is a composite number \(p=ab\) with \(a,b\) integers greater than \(1\). Then \(R\) has a zero divisor as we have \[0=p.1=(a.b).1=(a.1).(b.1).\]

What can we say of a ring \(R\) having zero divisors? It is known that the rings \(\mathbb{Z}/p.\mathbb{Z}\) where \(p\) is a prime are fields and therefore do not have zero divisors. Is this a general fact? That is, does a ring whose characteristic is a prime do not have zero divisors?

The answer is negative and we give below a counterexample.

Let’s consider the field \(\mathbb{F}_p = \mathbb{Z}/p.\mathbb{Z}\) where \(p\) is a prime and the product of rings \(R=\mathbb{F}_p \times \mathbb{F}_p\). One can verify following facts:

  • \(R\) additive identity is equal to \((0,0)\).
  • \(R\) multiplicative identity is equal to \((1,1)\).
  • \(R\) is commutative.
  • The characteristic of \(R\) is equal to \(p\) as for \(n\) integer, we have \(n.(1,1)=(n.1,n.1)\) which is equal to \((0,0)\) if and only if \(p\) divides \(n\).

However, \(R\) does have zero divisors as following identity holds: \[(1,0).(0,1)=(0,0)\]

Algebra

Two matrices A and B for which AB and BA have different minimal polynomials

Leave a comment

We consider here the algebra of matrices \(\mathcal{M}_n(\mathbb F)\) of dimension \(n \ge 1\) over a field \(\mathbb F\).

It is well known that for \(A,B \in \mathcal{M}_n(\mathbb F)\), the characteristic polynomial \(p_{AB}\) of the product \(AB\) is equal to the one (namely \(p_{BA}\)) of the product of \(BA\). What about the minimal polynomial?

Unlikely for the characteristic polynomials, the minimal polynomial \(\mu_{AB}\) of \(AB\) maybe different to the one of \(BA\).

Consider the two matrices \[
A=\begin{pmatrix}
0 & 1\\
0 & 0\end{pmatrix} \text{, }
B=\begin{pmatrix}
0 & 0\\
0 & 1\end{pmatrix}\] which can be defined whatever the field we consider: \(\mathbb R, \mathbb C\) or even a field of finite characteristic.

One can verify that \[
AB=A=\begin{pmatrix}
0 & 1\\
0 & 0\end{pmatrix} \text{, }
BA=\begin{pmatrix}
0 & 0\\
0 & 0\end{pmatrix}\]

As \(BA\) is the zero matrix, its minimal polynomial is \(\mu_{BA}=X\). Regarding the one of \(AB\), we have \((AB)^2=A^2=0\) hence \(\mu_{AB}\) divides \(X^2\). Moreover \(\mu_{AB}\) cannot be equal to \(X\) as \(AB \neq 0\). Finally \(\mu_{AB}=X^2\) and we verify that \[X^2=\mu_{AB} \neq \mu_{BA}=X.\]

Algebra

A finite extension that contains infinitely many subfields

Leave a comment

Let’s consider \(K/k\) a finite field extension of degree \(n\). The following theorem holds.

Theorem: the following conditions are equivalent:

  1. The extension contains a primitive element.
  2. The number of intermediate fields between \(k\) and \(K\) is finite.

Our aim here is to describe a finite field extension having infinitely many subfields. Considering the theorem above, we have to look at an extension without a primitive element.

The extension \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) is finite

For \(p\) prime, \(\mathbb F_p\) denotes the finite field with \(p\) elements. \(\mathbb F_p(X,Y)\) is the algebraic fraction field of two variables over the field \(\mathbb F_p\). \(\mathbb F_p(X^p,Y^p)\) is the subfield of \(\mathbb F_p(X,Y)\) generated by the elements \(X^p,Y^p\). Continue reading A finite extension that contains infinitely many subfields →

Algebra

A group isomorphic to its automorphism group

Leave a comment

We consider a group \(G\) and we look at its automorphism group \(\text{Aut}(G)\). Can \(G\) be isomorphic to
\(\text{Aut}(G)\)? The answer is positive and we’ll prove that it is the case for the symmetric group \(S_3\).

Consider the morphism \[
\begin{array}{l|rcl}
\Phi : & S_3 & \longrightarrow & \text{Aut}(S_3) \\
& a & \longmapsto & \varphi_a \end{array}\]
where \(\varphi_a\) is the inner automorphism \(\varphi_a : x \mapsto a^{-1}xa\). It is easy to verify that \(\Phi\) is indeed a group morphism. The kernel of \(\Phi\) is the center of \(S_3\) which is having the identity for only element. Hence \(\Phi\) is one-to-one and \(S_3 \simeq \Phi(S_3)\). Therefore it is sufficient to prove that \(\Phi\) is onto. As \(|S_3|=6\), we’ll be finished if we prove that \(|\text{Aut}(S_3)|=6\).

Generally, for \(G_1,G_2\) groups and \(f : G_1 \to G_2\) a one-to-one group morphism, the image of an element \(x\) of order \(k\) is an element \(f(x)\) having the same order \(k\). So for \(\varphi \in \text{Aut}(S_3)\) the image of a transposition is a transposition. As the transpositions \(\{(1 \ 2), (1 \ 3), (2 \ 3)\}\) generate \((S_3)\), \(\varphi\) is completely defined by \(\{\varphi((1 \ 2)), \varphi((1 \ 3)), \varphi((2 \ 3))\}\). We have 3 choices to define the image of \((1 \ 2)\) under \(\varphi\) and then 2 choices for the image of \((1 \ 3)\) under \(\varphi\). The image of \((2 \ 3)\) under \(\varphi\) is the remaining transposition.

Finally, we have proven that \(|\text{Aut}(S_3)|=6\) as desired and \(S_3 \simeq \text{Aut}(S_3)\).