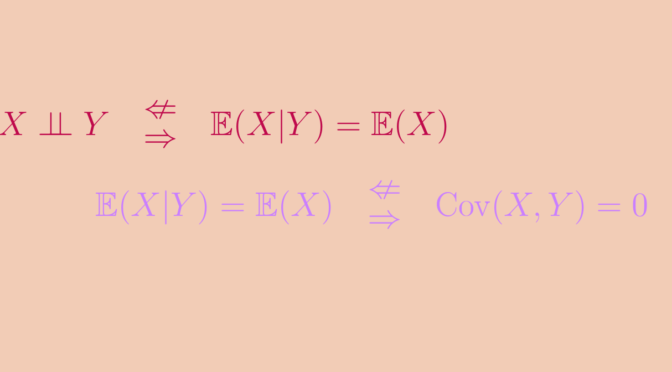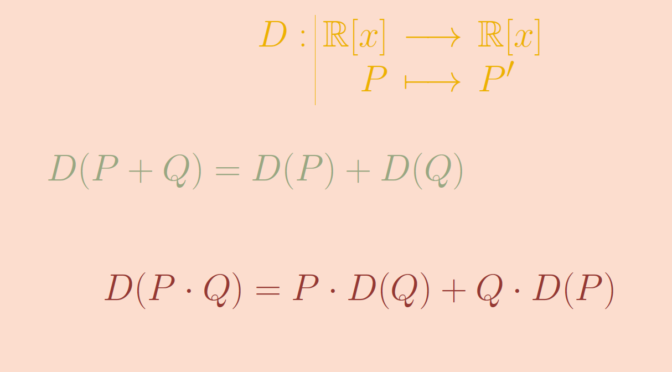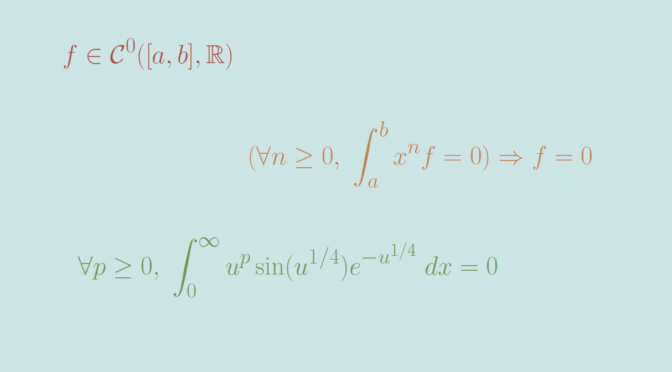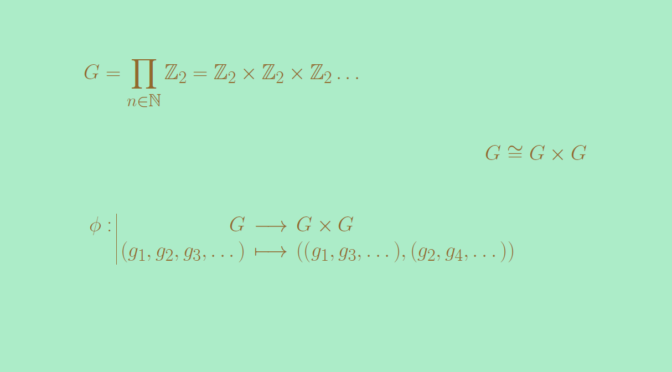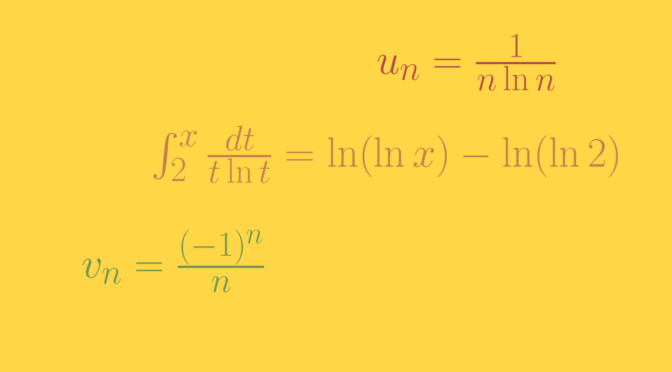Probability

Mean independent and correlated variables

1 Comment

Given two real random variables \(X\) and \(Y\), we say that:

  1. \(X\) and \(Y\) are independent if the events \(\{X \le x\}\) and \(\{Y \le y\}\) are independent for any \(x,y\),
  2. \(X\) is mean independent from \(Y\) if its conditional mean \(E(Y | X=x)\) equals its (unconditional) mean \(E(Y)\) for all \(x\) such that the probability that \(X = x\) is not zero,
  3. \(X\) and \(Y\) are uncorrelated if \(\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)\).

Assuming the necessary integrability hypothesis, we have the implications \(\ 1 \implies 2 \implies 3\).

The \(2^{\mbox{nd}}\) implication follows from the law of iterated expectations: \(\mathbb{E}(XY) = \mathbb{E}\big(\mathbb{E}(XY|Y)\big) = \mathbb{E}\big(\mathbb{E}(X|Y)Y\big) = \mathbb{E}(X)\mathbb{E}(Y)\)

Yet none of the reciprocals of these two implications are true.

Mean-independence without independence

Let \(\theta \sim \mbox{Unif}(0,2\pi)\), and \((X,Y)=\big(\cos(\theta),\sin(\theta)\big)\).

Then for all \(y \in [-1,1]\), conditionally to \(Y=y\), \(X\) follows a uniform distribution on \(\{-\sqrt{1-y^2},\sqrt{1-y^2}\}\), so: \[\mathbb{E}(X|Y=y)=0=\mathbb{E}(X).\] Likewise, we have \(\mathbb{E}(Y|X) = 0\).

Yet \(X\) and \(Y\) are not independent. Indeed, \(\mathbb{P}(X>0.75)>0\)  and \(\mathbb{P}(Y>0.75) > 0\), but  \(\mathbb{P}(X>0.75, Y>0.75) = 0\) because \(X^2+Y^2 = 1\) and \(0.75^2 + 0.75^2 > 1\).

Uncorrelation without mean-independence

A simple counterexample is \((X,Y)\) uniformly distributed on the vertices of a regular polygon centered on the origin, not symmetric with respect to either axis.

For example, let \((X, Y)\) have uniform distribution with values in \[\big\{(1,3), (-3,1), (-1,-3), (3,-1)\big\}.\]

Then \(\mathbb{E}(XY) = 0\) and \(\mathbb{E}(X)=\mathbb{E}(Y)=0\), so \(X\) and \(Y\) are uncorrelated.

Yet \(\mathbb{E}(X|Y=1) = -3\), \(\mathbb{E}(X|Y=3)=1\) so we don’t have \(\mathbb{E}(X|Y) = \mathbb{E}(X)\). Likewise, we don’t have \(\mathbb{E}(Y|X) = \mathbb{E}(Y)\).

Topology

Separability of a vector space and its dual

Leave a comment

Let’s recall that a topological space is separable when it contains a countable dense set. A link between separability and the dual space is following theorem:

Theorem: If the dual \(X^*\) of a normed vector space \(X\) is separable, then so is the space \(X\) itself.

Proof outline: let \({f_n}\) be a countable dense set in \(X^*\) unit sphere \(S_*\). For any \(n \in \mathbb{N}\) one can find \(x_n\) in \(X\) unit ball such that \(f_n(x_n) \ge \frac{1}{2}\). We claim that the countable set \(F = \mathrm{Span}_{\mathbb{Q}}(x_0,x_1,…)\) is dense in \(X\). If not, we would find \(x \in X \setminus \overline{F}\) and according to Hahn-Banach theorem there would exist a linear functional \(f \in X^*\) such that \(f_{\overline{F}} = 0\) and \(\Vert f \Vert=1\). But then for all \(n \in \mathbb{N}\), \(\Vert f_n-f \Vert \ge \vert f_n(x_n)-f(x_n)\vert = \vert f_n(x_n) \vert \ge \frac{1}{2}\). A contradiction since \({f_n}\) is supposed to be dense in \(S_*\).

We prove that the converse is not true, i.e. a dual space can be separable, while the space itself may be separable or not.

Introducing some normed vector spaces

Given a closed interval \(K \subset \mathbb{R}\) and a set \(A \subset \mathbb{R}\), we define the \(4\) following spaces. The first three are endowed with the supremum norm, the last one with the \(\ell^1\) norm.

  • \(\mathcal{C}(K,\mathbb{R})\), the space of continuous functions from \(K\) to \(\mathbb{R}\), is separable as the polynomial functions with coefficients in \(\mathbb{Q}\) are dense and countable.
  • \(\ell^{\infty}(A, \mathbb{R})\) is the space of real bounded functions defined on \(A\) with countable support.
  • \(c_0(A, \mathbb{R}) \subset \ell^{\infty}(A, \mathbb{R})\) is the subspace of elements of \(\ell^{\infty}(A)\) going to \(0\) at \(\infty\).
  • \(\ell^1(A, \mathbb{R})\) is the space of summable functions on \(A\): \(u \in \mathbb{R}^{A}\) is in \(\ell^1(A, \mathbb{R})\) iff \(\sum \limits_{a \in A} |u_x| < +\infty\).

When \(A = \mathbb{N}\), we find the usual sequence spaces. It should be noted that \(c_0(A, \mathbb{R})\) and \(\ell^1(A, \mathbb{R})\) are separable iff \(A\) is countable (otherwise the subset \(\big\{x \mapsto 1_{\{a\}}(x),\ a \in A \big\}\) is uncountable, and discrete), and that \(\ell^{\infty}(A, \mathbb{R})\) is separable iff \(A\) is finite (otherwise the subset \(\{0,1\}^A\) is uncountable, and discrete).

Continue reading Separability of a vector space and its dual →
Probability

Determinacy of random variables

Leave a comment

The question of the determinacy (or uniqueness) in the moment problem consists in finding whether the moments of a real-valued random variable determine uniquely its distribution. If we assume the random variable to be a.s. bounded, uniqueness is a consequence of Weierstrass approximation theorem.

Given the moments, the distribution need not be unique for unbounded random variables. Carleman’s condition states that for two positive random variables \(X, Y\) with the same finite moments for all orders, if \(\sum\limits_{n \ge 1} \frac{1}{\sqrt[2n]{\mathbb{E}(X^n)}} = +\infty\), then \(X\) and \(Y\) have the same distribution. In this article we describe random variables with different laws but sharing the same moments, on \(\mathbb R_+\) and \(\mathbb N\).

Continuous case on \(\mathbb{R}_+\)

In the article a non-zero function orthogonal to all polynomials, we described a function \(f\) orthogonal to all polynomials in the sense that \[
\forall k \ge 0,\ \displaystyle{\int_0^{+\infty}} x^k f(x)dx = 0 \tag{O}.\]

This function was \(f(u) = \sin\big(u^{\frac{1}{4}}\big)e^{-u^{\frac{1}{4}}}\). This inspires us to define \(U\) and \(V\) with values in \(\mathbb R^+\) by: \[\begin{cases}
f_U(u) &= \frac{1}{24}e^{-\sqrt[4]{u}}\\
f_V(u) &= \frac{1}{24}e^{-\sqrt[4]{u}} \big( 1 + \sin(\sqrt[4]{u})\big)
\end{cases}\]

Both functions are positive. Since \(f\) is orthogonal to the constant map equal to one and \(\displaystyle{\int_0^{+\infty}} f_U = \displaystyle{\int_0^{+\infty}} f_V = 1\), they are indeed densities. One can verify that \(U\) and \(V\) have moments of all orders and \(\mathbb{E}(U^k) = \mathbb{E}(V^k)\) for all \(k \in \mathbb N\) according to orthogonality relation \((\mathrm O)\) above.

Discrete case on \(\mathbb N\)

In this section we define two random variables \(X\) and \(Y\) with values in \(\mathbb N\) having the same moments. Let’s take an integer \(q \ge 2\) and set for all \(n \in \mathbb{N}\): \[
\begin{cases}
\mathbb{P}(X=q^n) &=e^{-q}q^n \cdot \frac{1}{n!} \\
\mathbb{P}(Y=q^n) &= e^{-q}q^n\left(\frac{1}{n!} + \frac{(-1)^n}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\right)
\end{cases}\]

Both quantities are positive and for any \(k \ge 0\), \(\mathbb{P}(X=q^n)\) and \(\mathbb{P}(Y=q^n) = O_{n \to \infty}\left(\frac{1}{q^{kn}}\right)\). We are going to prove that for all \(k \ge 1\), \( u_k = \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn}}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\) is equal to \(0\).

Continue reading Determinacy of random variables →
Algebra

Group homomorphism versus ring homomorphism

Leave a comment

A ring homomorphism is a function between two rings which respects the structure. Let’s provide examples of functions between rings which respect the addition or the multiplication but not both.

An additive group homomorphism that is not a ring homomorphism

We consider the ring \(\mathbb R[x]\) of real polynomials and the derivation \[
\begin{array}{l|rcl}
D : & \mathbb R[x] & \longrightarrow & \mathbb R[x] \\
& P & \longmapsto & P^\prime \end{array}\] \(D\) is an additive homomorphism as for all \(P,Q \in \mathbb R[x]\) we have \(D(P+Q) = D(P) + D(Q)\). However, \(D\) does not respect the multiplication as \[
D(x^2) = 2x \neq 1 = D(x) \cdot D(x).\] More generally, \(D\) satisfies the Leibniz rule \[
D(P \cdot Q) = P \cdot D(Q) + Q \cdot D(P).\]

A multiplication group homomorphism that is not a ring homomorphism

The function \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is a multiplicative group homomorphism of the group \((\mathbb R, \cdot)\). However \(f\) does not respect the addition.

Analysis

A nonzero continuous map orthogonal to all polynomials

1 Comment

Let’s consider the vector space \(\mathcal{C}^0([a,b],\mathbb R)\) of continuous real functions defined on a compact interval \([a,b]\). We can define an inner product on pairs of elements \(f,g\) of \(\mathcal{C}^0([a,b],\mathbb R)\) by \[
\langle f,g \rangle = \int_a^b f(x) g(x) \ dx.\]

It is known that \(f \in \mathcal{C}^0([a,b],\mathbb R)\) is the always vanishing function if we have \(\langle x^n,f \rangle = \int_a^b x^n f(x) \ dx = 0\) for all integers \(n \ge 0\). Let’s recall the proof. According to Stone-Weierstrass theorem, for all \(\epsilon >0\) it exists a polynomial \(P\) such that \(\Vert f – P \Vert_\infty \le \epsilon\). Then \[
\begin{aligned}
0 &\le \int_a^b f^2 = \int_a^b f(f-P) + \int_a^b fP\\
&= \int_a^b f(f-P) \le \Vert f \Vert_\infty \epsilon(b-a)
\end{aligned}\] As this is true for all \(\epsilon > 0\), we get \(\int_a^b f^2 = 0\) and \(f = 0\).

We now prove that the result becomes false if we change the interval \([a,b]\) into \([0, \infty)\), i.e. that one can find a continuous function \(f \in \mathcal{C}^0([0,\infty),\mathbb R)\) such that \(\int_0^\infty x^n f(x) \ dx\) for all integers \(n \ge 0\). In that direction, let’s consider the complex integral \[
I_n = \int_0^\infty x^n e^{-(1-i)x} \ dx.\] \(I_n\) is well defined as for \(x \in [0,\infty)\) we have \(\vert x^n e^{-(1-i)x} \vert = x^n e^{-x}\) and \(\int_0^\infty x^n e^{-x} \ dx\) converges. By integration by parts, one can prove that \[
I_n = \frac{n!}{(1-i)^{n+1}} = \frac{(1+i)^{n+1}}{2^{n+1}} n! = \frac{e^{i \frac{\pi}{4}(n+1)}}{2^{\frac{n+1}{2}}}n!.\] Consequently, \(I_{4p+3} \in \mathbb R\) for all \(p \ge 0\) which means \[
\int_0^\infty x^{4p+3} \sin(x) e^{-x} \ dx =0\] and finally \[
\int_0^\infty u^p \sin(u^{1/4}) e^{-u^{1/4}} \ dx =0\] for all integers \(p \ge 0\) using integration by substitution with \(x = u^{1/4}\). The function \(u \mapsto \sin(u^{1/4}) e^{-u^{1/4}}\) is one we were looking for.

Algebra

A group G isomorph to the product group G x G

Leave a comment

Let’s provide an example of a nontrivial group \(G\) such that \(G \cong G \times G\). For a finite group \(G\) of order \(\vert G \vert =n > 1\), the order of \(G \times G\) is equal to \(n^2\). Hence we have to look at infinite groups in order to get the example we’re seeking for.

We take for \(G\) the infinite direct product \[
G = \prod_{n \in \mathbb N} \mathbb Z_2 = \mathbb Z_2 \times \mathbb Z_2 \times \mathbb Z_2 \dots,\] where \(\mathbb Z_2\) is endowed with the addition. Now let’s consider the map \[
\begin{array}{l|rcl}
\phi : & G & \longrightarrow & G \times G \\
& (g_1,g_2,g_3, \dots) & \longmapsto & ((g_1,g_3, \dots ),(g_2, g_4, \dots)) \end{array}\]

From the definition of the addition in \(G\) it follows that \(\phi\) is a group homomorphism. \(\phi\) is onto as for any element \(\overline{g}=((g_1, g_2, g_3, \dots),(g_1^\prime, g_2^\prime, g_3^\prime, \dots))\) in \(G \times G\), \(g = (g_1, g_1^\prime, g_2, g_2^\prime, \dots)\) is an inverse image of \(\overline{g}\) under \(\phi\). Also the identity element \(e=(\overline{0},\overline{0}, \dots)\) of \(G\) is the only element of the kernel of \(G\). Hence \(\phi\) is also one-to-one. Finally \(\phi\) is a group isomorphism between \(G\) and \(G \times G\).

Analysis

Counterexamples around series (part 1)

1 Comment

The purpose of this article is to provide some basic counterexamples on real series. Counterexamples are provided as answers to questions.

Unless otherwise stated, \((u_n)_{n \in \mathbb{N}}\) and \((v_n)_{n \in \mathbb{N}}\) are two real sequences.

If \((u_n)\) is non-increasing and converges to zero then \(\sum u_n\) converges?

Is not true. A famous counterexample is the harmonic series \(\sum \frac{1}{n}\) which doesn’t converge as \[
\displaystyle \sum_{k=p+1}^{2p} \frac{1}{k} \ge \sum_{k=p+1}^{2p} \frac{1}{2p} = 1/2,\] for all \(p \in \mathbb N\).

If \(u_n = o(1/n)\) then \(\sum u_n\) converges?

Does not hold as can be seen considering \(u_n=\frac{1}{n \ln n}\) for \(n \ge 2\). Indeed \(\int_2^x \frac{dt}{t \ln t} = \ln(\ln x) – \ln (\ln 2)\) and therefore \(\int_2^\infty \frac{dt}{t \ln t}\) diverges. We conclude that \(\sum \frac{1}{n \ln n}\) diverges using the integral test. However \(n u_n = \frac{1}{\ln n}\) converges to zero. Continue reading Counterexamples around series (part 1) →

Algebra

Isomorphism of factors does not imply isomorphism of quotient groups

Leave a comment

Let \(G\) be a group and \(H, K\) two isomorphic subgroups. We provide an example where the quotient groups \(G / H\) and \(G / K\) are not isomorphic.

Let \(G = \mathbb{Z}_4 \times \mathbb{Z}_2\), with \(H = \langle (\overline{2}, \overline{0}) \rangle\) and \(K = \langle (\overline{0}, \overline{1}) \rangle\). We have \[
H \cong K \cong \mathbb{Z}_2.\] The left cosets of \(H\) in \(G\) are \[
G / H=\{(\overline{0}, \overline{0}) + H, (\overline{1}, \overline{0}) + H, (\overline{0}, \overline{1}) + H, (\overline{1}, \overline{1}) + H\},\] a group having \(4\) elements and for all elements \(x \in G/H\), one can verify that \(2x = H\). Hence \(G / H \cong \mathbb{Z}_2 \times \mathbb{Z}_2\). The left cosets of \(K\) in \(G\) are \[
G / K=\{(\overline{0}, \overline{0}) + K, (\overline{1}, \overline{0}) + K, (\overline{2}, \overline{0}) + K, (\overline{3}, \overline{0}) + K\},\] which is a cyclic group of order \(4\) isomorphic to \(\mathbb{Z}_4\). We finally get the desired conclusion \[
G / H \cong \mathbb{Z}_2 \times \mathbb{Z}_2 \ncong \mathbb{Z}_4 \cong G / K.\]

Set Theory

An uncountable chain of subsets of the natural numbers

Leave a comment

Consider the set \(\mathcal P(\mathbb N)\) of the subsets of the natural integers \(\mathbb N\). \(\mathcal P(\mathbb N)\) is endowed with the strict order \(\subset\). Let’s have a look to the chains of \((\mathcal P(\mathbb N),\subset)\), i.e. to the totally ordered subsets \(S \subset \mathcal P(\mathbb N)\).

Some finite chains

It is easy to produce some finite chains like \(\{\{1\}, \{1,2\},\{1,2,3\}\}\) or one with a length of size \(n\) where \(n\) is any natural number like \[
\{\{1\}, \{1,2\}, \dots, \{1,2, \dots, n\}\}\] or \[
\{\{1\}, \{1,2^2\}, \dots, \{1,2^2, \dots, n^2\}\}\]

Some infinite countable chains

It’s not much complicated to produce some countable infinite chains like \[
\{\{1 \},\{1,2 \},\{1,2,3\},…,\mathbb{N}\}\] or \[
\{\{5 \},\{5,6 \},\{5,6,7\},…,\mathbb N \setminus \{1,2,3,4\} \}\]

Let’s go further and define a one-to-one map from the real interval \([0,1)\) into the set of countable chains of \((\mathcal P(\mathbb N),\subset)\). For \(x \in [0,1)\) let \(\displaystyle x = \sum_{i=1}^\infty x_i 2^{-i}\) be its binary representation. For \(n \in \mathbb N\) we define \(S_n(x) = \{k \in \mathbb N \ ; \ k \le n \text{ and } x_k = 1\}\). It is easy to verify that \(\left(S_n(x))_{n \in \mathbb N}\right)\) is a countable chain of \((\mathcal P(\mathbb N),\subset)\) and that \(\left(S_n(x))\right) \neq \left(S_n(x^\prime))\right)\) for \(x \neq x^\prime\).

What about defining an uncountable chain? Continue reading An uncountable chain of subsets of the natural numbers →

Mathematical exceptions to the rules or intuition