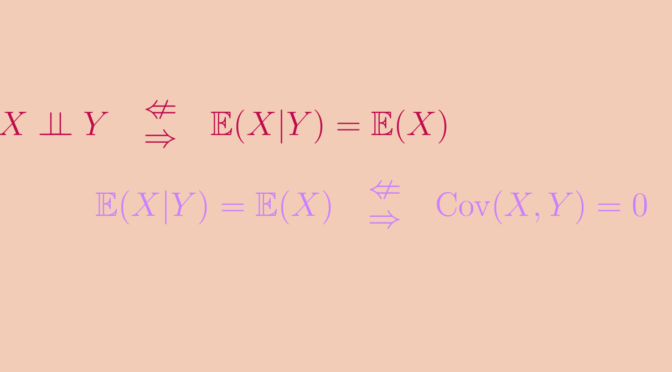Given two real random variables \(X\) and \(Y\), we say that:
- \(X\) and \(Y\) are independent if the events \(\{X \le x\}\) and \(\{Y \le y\}\) are independent for any \(x,y\),
- \(X\) is mean independent from \(Y\) if its conditional mean \(E(Y | X=x)\) equals its (unconditional) mean \(E(Y)\) for all \(x\) such that the probability that \(X = x\) is not zero,
- \(X\) and \(Y\) are uncorrelated if \(\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)\).
Assuming the necessary integrability hypothesis, we have the implications \(\ 1 \implies 2 \implies 3\).
The \(2^{\mbox{nd}}\) implication follows from the law of iterated expectations: \(\mathbb{E}(XY) = \mathbb{E}\big(\mathbb{E}(XY|Y)\big) = \mathbb{E}\big(\mathbb{E}(X|Y)Y\big) = \mathbb{E}(X)\mathbb{E}(Y)\)
Yet none of the reciprocals of these two implications are true.
Mean-independence without independence
Let \(\theta \sim \mbox{Unif}(0,2\pi)\), and \((X,Y)=\big(\cos(\theta),\sin(\theta)\big)\).
Then for all \(y \in [-1,1]\), conditionally to \(Y=y\), \(X\) follows a uniform distribution on \(\{-\sqrt{1-y^2},\sqrt{1-y^2}\}\), so: \[\mathbb{E}(X|Y=y)=0=\mathbb{E}(X).\] Likewise, we have \(\mathbb{E}(Y|X) = 0\).
Yet \(X\) and \(Y\) are not independent. Indeed, \(\mathbb{P}(X>0.75)>0\) and \(\mathbb{P}(Y>0.75) > 0\), but \(\mathbb{P}(X>0.75, Y>0.75) = 0\) because \(X^2+Y^2 = 1\) and \(0.75^2 + 0.75^2 > 1\).
Uncorrelation without mean-independence
A simple counterexample is \((X,Y)\) uniformly distributed on the vertices of a regular polygon centered on the origin, not symmetric with respect to either axis.
For example, let \((X, Y)\) have uniform distribution with values in \[\big\{(1,3), (-3,1), (-1,-3), (3,-1)\big\}.\]
Then \(\mathbb{E}(XY) = 0\) and \(\mathbb{E}(X)=\mathbb{E}(Y)=0\), so \(X\) and \(Y\) are uncorrelated.
Yet \(\mathbb{E}(X|Y=1) = -3\), \(\mathbb{E}(X|Y=3)=1\) so we don’t have \(\mathbb{E}(X|Y) = \mathbb{E}(X)\). Likewise, we don’t have \(\mathbb{E}(Y|X) = \mathbb{E}(Y)\).