Consider a first order linear differential equation \[
y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B\) are real continuous functions defined on a non-empty real interval \(I\). According to Picard-Lindelöf theorem, the initial value problem \[
\begin{cases}
y^\prime(x) = A(x)y(x) + B(x)\\
y(x_0) = y_0, \ x_0 \in I
\end{cases}\] has a unique solution defined on \(I\).
However, a linear differential equation \[
c(x)y^\prime(x) = A(x)y(x) + B(x)\] where \(A, B, c\) are real continuous functions might not have a solution to an initial value problem. Let’s have a look at the equation \[
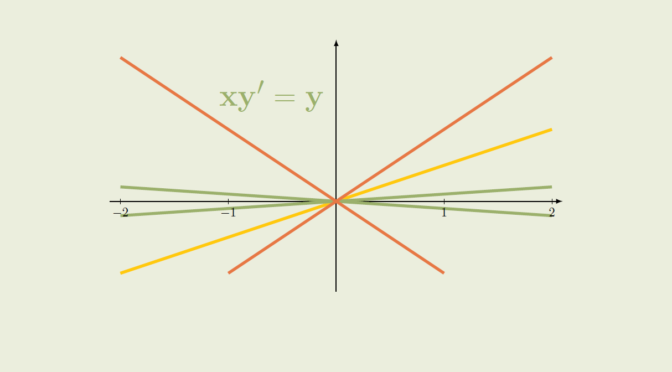
x y^\prime(x) = y(x) \tag{E}\label{eq:IVP}\] for \(x \in \mathbb R\). The equation is linear.
For \(x \in (-\infty,0)\) a solution to \eqref{eq:IVP} is a solution of the explicit differential linear equation \[
y^\prime(x) = \frac{y(x)}x\] hence can be written \(y(x) = \lambda_-x\) with \(\lambda_- \in \mathbb R\). Similarly, a solution to \eqref{eq:IVP} on the interval \((0,\infty)\) is of the form \(y(x) = \lambda_+ x\) with \(\lambda_+ \in \mathbb R\).
A global solution to \eqref{eq:IVP}, i.e. defined on the whole real line is differentiable at \(0\) hence the equation \[
\lambda_- = y_-^\prime(0)=y_+^\prime(0) = \lambda_+\] which means that \(y(x) = \lambda x\) where \(\lambda=\lambda_-=\lambda_+\).
In particular all solutions defined on \(\mathbb R\) are such that \(y(0)=0\). Therefore the initial value problem \[
\begin{cases}
x y^\prime(x) = y(x)\\
y(0)=1
\end{cases}\] has no solution.