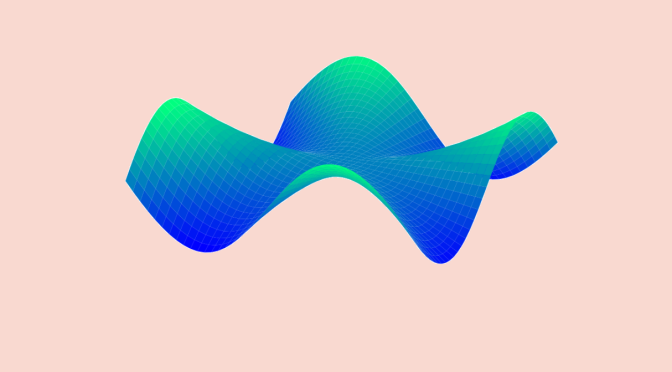
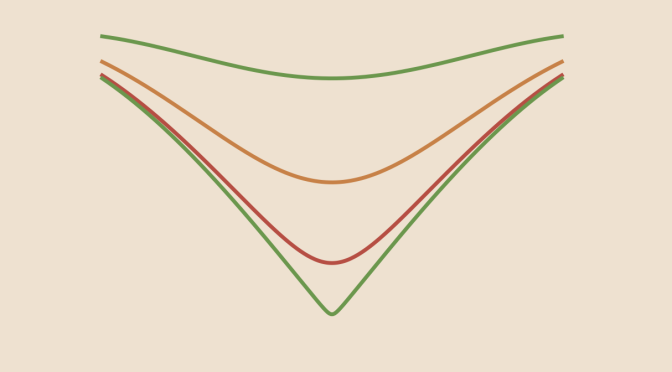
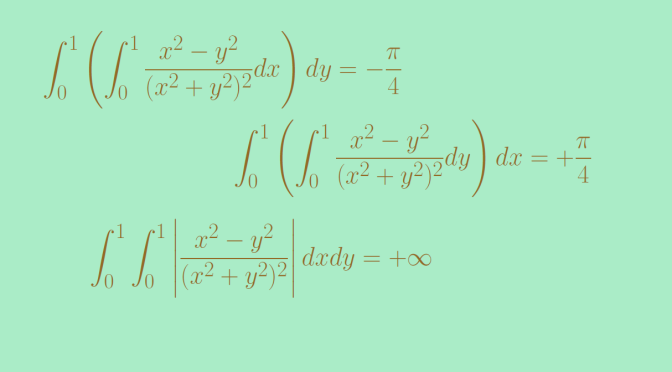Tag Archives: analysis

Analysis

No minimum at the origin but a minimum along all lines

Leave a comment

We look here at an example, from the Italian mathematician Giuseppe Peano of a real function \(f\) defined on \(\mathbb{R}^2\). \(f\) is having a local minimum at the origin along all lines passing through the origin, however \(f\) does not have a local minimum at the origin as a function of two variables.

The function \(f\) is defined as follows
\[\begin{array}{l|rcl}
f : & \mathbb{R}^2 & \longrightarrow & \mathbb{R} \\
& (x,y) & \longmapsto & f(x,y)=3x^4-4x^2y+y^2 \end{array}\] One can notice that \(f(x, y) = (y-3x^2)(y-x^2)\). In particular, \(f\) is strictly negative on the open set \(U=\{(x,y) \in \mathbb{R}^2 \ : \ x^2 < y < 3x^2\}\), vanishes on the parabolas \(y=x^2\) and \(y=3 x^2\) and is strictly positive elsewhere. Consider a line \(D\) passing through the origin. If \(D\) is different from the coordinate axes, the equation of \(D\) is \(y = \lambda x\) with \(\lambda > 0\). We have \[f(x, \lambda x)= x^2(\lambda-3x)(\lambda -x).\] For \(x \in (-\infty,\frac{\lambda}{3}) \setminus \{0\}\), \(f(x, \lambda x) > 0\) while \(f(0,0)=0\) which proves that \(f\) has a local minimum at the origin along the line \(D \equiv y – \lambda x=0\). Along the \(x\)-axis, we have \(f(x,0)=3 x^ 4\) which has a minimum at the origin. And finally, \(f\) also has a minimum at the origin along the \(y\)-axis as \(f(0,y)=y^2\).

However, along the parabola \(\mathcal{P} \equiv y = 2 x^2\) we have \(f(x,2 x^2)=-x^4\) which is strictly negative for \(x \neq 0\). As \(\mathcal{P}\) is passing through the origin, \(f\) assumes both positive and negative values in all neighborhood of the origin.

This proves that \(f\) does not have a minimum at \((0,0)\).

Analysis

Counterexamples around Fubini’s theorem

Leave a comment

We present here some counterexamples around the Fubini theorem.

We recall Fubini’s theorem for integrable functions:
let \(X\) and \(Y\) be \(\sigma\)-finite measure spaces and suppose that \(X \times Y\) is given the product measure. Let \(f\) be a measurable function for the product measure. Then if \(f\) is \(X \times Y\) integrable, which means that \(\displaystyle \int_{X \times Y} \vert f(x,y) \vert d(x,y) < \infty\), we have \[\int_X \left( \int_Y f(x,y) dy \right) dx = \int_Y \left( \int_X f(x,y) dx \right) dy = \int_{X \times Y} f(x,y) d(x,y)\] Let's see what happens when some hypothesis of Fubini's theorem are not fulfilled. Continue reading Counterexamples around Fubini’s theorem →

Analysis

Differentiability of multivariable real functions (part2)

Leave a comment

Following the article on differentiability of multivariable real functions (part 1), we look here at second derivatives. We consider a function \(f : \mathbb R^n \to \mathbb R\) with \(n \ge 2\).

Schwarz’s theorem states that if \(f : \mathbb R^n \to \mathbb R\) has continuous second partial derivatives at any given point in \(\mathbb R^n\), then for \((a_1, \dots, a_n) \in \mathbb R^n\) and \(i,j \in \{1, \dots, n\}\):
\[\frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, \dots, a_n)=\frac{\partial^2 f}{\partial x_j \partial x_i}(a_1, \dots, a_n)\]

A function for which \(\frac{\partial^2 f}{\partial x \partial y}(0,0) \neq \frac{\partial^2 f}{\partial y \partial x}(0,0)\)

We consider:
\[\begin{array}{l|rcl}
f : & \mathbb R^2 & \longrightarrow & \mathbb R \\
& (0,0) & \longmapsto & 0\\
& (x,y) & \longmapsto & \frac{xy(x^2-y^2)}{x^2+y^2} \text{ for } (x,y) \neq (0,0)
\end{array}\] Continue reading Differentiability of multivariable real functions (part2) →

Analysis

A discontinuous real convex function

Leave a comment

Consider a function \(f\) defined on a real interval \(I \subset \mathbb R\). \(f\) is called convex if: \[\forall x, y \in I \ \forall \lambda \in [0,1]: \ f((1-\lambda)x+\lambda y) \le (1-\lambda) f(x) + \lambda f(y)\]

Suppose that \(I\) is a closed interval: \(I=[a,b]\) with \(a < b\). For \(a < s < t < u < b\) one can prove that: \[\frac{f(t)-f(s)}{t-s}\le \frac{f(u)-f(s)}{u-s}\le\frac{f(u)-f(t)}{u-t}.\] It follows from those relations that \(f\) has left-hand and right-hand derivatives at each point of the interior of \(I\). And therefore that \(f\) is continuous at each point of the interior of \(I\).
Is a convex function defined on an interval \(I\) continuous at all points of the interval? That might not be the case and a simple example is the function: \[\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & \mathbb R \\
& x & \longmapsto & 0 \text{ for } x \in (0,1) \\
& x & \longmapsto & 1 \text{ else}\end{array}\]

It can be easily verified that \(f\) is convex. However, \(f\) is not continuous at \(0\) and \(1\).

Analysis

Differentiability of multivariable real functions (part1)

2 Comments

This article provides counterexamples about differentiability of functions of several real variables. We focus on real functions of two real variables (defined on \(\mathbb R^2\)). \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall some definitions and theorems about differentiability of functions of several real variables.

Definition 1 We say that a function \(f : \mathbb R^2 \to \mathbb R\) is differentiable at \(\mathbf{a} \in \mathbb R^2\) if it exists a (continuous) linear map \(\nabla f(\mathbf{a}) : \mathbb R^2 \to \mathbb R\) with \[\lim\limits_{\mathbf{h} \to 0} \frac{f(\mathbf{a}+\mathbf{h})-f(\mathbf{a})-\nabla f(\mathbf{a}).\mathbf{h}}{\Vert \mathbf{h} \Vert} = 0\]

Definition 2 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. Then the \(\mathbf{i^{th}}\) partial derivative at point \(\mathbf{a}\) is the real number
\begin{align*}
\frac{\partial f}{\partial x_i}(\mathbf{a}) &= \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{e_i})- f(\mathbf{a})}{h}\\
&= \lim\limits_{h \to 0} \frac{f(a_1,\dots,a_{i-1},a_i+h,a_{i+1},\dots,a_n) – f(a_1,\dots,a_{i-1},a_i,a_{i+1},\dots,a_n)}{h}
\end{align*} For two real variable functions, \(\frac{\partial f}{\partial x}(x,y)\) and \(\frac{\partial f}{\partial y}(x,y)\) will denote the partial derivatives.

Definition 3 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. The directional derivative of \(f\) along vector \(\mathbf{v}\) at point \(\mathbf{a}\) is the real \[\nabla_{\mathbf{v}}f(\mathbf{a}) = \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{v})- f(\mathbf{a})}{h}\] Continue reading Differentiability of multivariable real functions (part1) →

Analysis

Continuity of multivariable real functions

1 Comment

This article provides counterexamples about continuity of functions of several real variables. In addition the article discusses the cases of functions of two real variables (defined on \(\mathbb R^2\) having real values. \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall that a function \(f\) defined from \(\mathbb R^2\) to \(\mathbb R\) is continuous at \((x_0,y_0) \in \mathbb R^2\) if for any \(\epsilon > 0\), there exists \(\delta > 0\), such that \(\Vert (x,y) -(x_0,y_0) \Vert < \delta \Rightarrow \vert f(x,y) - f(x_0,y_0) \vert < \epsilon\). Continue reading Continuity of multivariable real functions →

Analysis

Counterexamples on function limits (part 1)

Leave a comment

Let \(f\) and \(g\) be two real functions and \(a \in \mathbb R \cup \{+\infty\}\). We provide here examples and counterexamples regarding the limits of \(f\) and \(g\).

If \(f\) has a limit as \(x\) tends to \(a\) then \(\vert f \vert\) also?

This is true. It is a consequence of the reverse triangle inequality \[\left\vert \vert f(x) \vert – \vert l \vert \right\vert \le \vert f(x) – l \vert\] Hence if \(\displaystyle \lim\limits_{x \to a} f(x) = l\), \(\displaystyle \lim\limits_{x \to a} \vert f(x) \vert = \vert l \vert\)

Is the converse of previous statement also true?

It is not. Consider the function defined by: \[\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& \frac{1}{n} & \longmapsto & -1 \text{ for } n \ge 1 \text{ integer} \\
& x & \longmapsto & 1 \text{ otherwise} \end{array}\] \(\vert f \vert\) is the constant function equal to \(1\), hence \(\vert f \vert\) has \(1\) for limit as \(x\) tends to zero. However \(\lim\limits_{x \to 0} f(x)\) doesn’t exist. Continue reading Counterexamples on function limits (part 1) →

Analysis

Counterexamples around differentiation of sequences of functions

Leave a comment

We consider here sequences of real functions defined on a closed interval. Following theorem is the main one regarding the differentiation of the limit.

Theorem: Suppose \((f_n)\) is a sequence of functions, differentiable on \([a,b]\) and such that \((f_n(x_0))\) converges for some point \(x_0 \in [a,b]\). If \((f_n^\prime)\) converges uniformly on \([a,b]\), then \((f_n)\) converges uniformly on \([a,b]\) to a function \(f\) and for all \(x \in [a,b]\) \[f^\prime(x)=\lim\limits_{n \to \infty} f_n^\prime(x)\] What happens if we drop some hypothesis of the theorem? Continue reading Counterexamples around differentiation of sequences of functions →

Analysis

Pointwise convergence and properties of the limit (part 1)

Leave a comment

We look here at the continuity of a sequence of functions that converges pointwise and give some counterexamples of what happens versus uniform convergence.

Recalling the definition of pointwise convergence

We consider here real functions defined on a closed interval \([a,b]\). A sequence of functions \((f_n)\) defined on \([a,b]\) converges pointwise to the function \(f\) if and only if for all \(x \in [a,b]\) \(\displaystyle \lim\limits_{n \to +\infty} f_n(x) = f(x)\). Pointwise convergence is weaker than uniform convergence.

Pointwise convergence does not, in general, preserve continuity

Suppose that \(f_n \ : \ [0,1] \to \mathbb{R}\) is defined by \(f_n(x)=x^n\). For \(0 \le x <1\) then \(\displaystyle \lim\limits_{n \to +\infty} x^n = 0\), while if \(x = 1\) then \(\displaystyle \lim\limits_{n \to +\infty} x^n = 1\). Hence the sequence \(f_n\) converges to the function equal to \(0\) for \(0 \le x < 1\) and to \(1\) for \(x=1\). Although each \(f_n\) is a continuous function of \([0,1]\), their pointwise limit is not. \(f\) is discontinuous at \(1\). We notice that \((f_n)\) doesn't converge uniformly to \(f\) as for all \(n \in \mathbb{N}\), \(\displaystyle \sup\limits_{x \in [0,1]} \vert f_n(x) - f(x) \vert = 1\). That's reassuring as uniform convergence of a sequence of continuous functions implies that the limit is continuous! Continue reading Pointwise convergence and properties of the limit (part 1) →

Analysis

A nowhere locally bounded function

1 Comment

In that article, I described some properties of Thomae’s function\(f\). Namely:

  • The function is discontinuous on \(\mathbb{Q}\).
  • Continuous on \(\mathbb{R} \setminus \mathbb{Q}\).
  • Its right-sided and left-sided limits vanish at all points.

Let’s modify \(f\) to get function \(g\) defined as follow:
\[g:
\left|\begin{array}{lrl}
\mathbb{R} & \longrightarrow & \mathbb{R} \\
x & \longmapsto & 0 \text{ if } x \in \mathbb{R} \setminus \mathbb{Q} \\
\frac{p}{q} & \longmapsto & q \text{ if } \frac{p}{q} \text{ in lowest terms and } q > 0
\end{array}\right.\] \(f\) and \(g\) both vanish on the set of irrational numbers, while on the set of rational numbers, \(g\) is equal to the reciprocal of \(f\). We now consider an open subset \(O \subset \mathbb{R}\) and \(x \in O\). As \(f\) right-sided and left-sided limits vanish at all points, we have \(\lim\limits_{n \to +\infty} f(x_n) = 0\) for all sequence \((x_n)\) of rational numbers converging to \(x\) (and such a sequence exists as the rational numbers are everywhere dense in the reals). Hence \(\lim\limits_{n \to +\infty} g(x_n) = + \infty\) as \(f\) is positive.

We can conclude that \(g\) is nowhere locally bounded. The picture of the article is a plot of function \(g\) on the rational numbers \(r = \frac{p}{q}\) in lowest terms for \(0 < r < 1\) and \(q \le 50\).