Can the symmetric group \(\mathcal{S}_n\) be generated by any transposition and any \(n\)-cycle for \(n \ge 2\) integer? is the question we deal with.

We first recall some terminology:

Symmetric group

The symmetric group \(\mathcal{S}_n\) on a finite set of \(n\) symbols is the group whose elements are all the permutations of the \(n\) symbols. We’ll denote by \(\{1,\dots,n\}\) those \(n\) symbols.

Cycle

A cycle of length \(k\) (with \(k \ge 2\)) is a cyclic permutation \(\sigma\) for which there exists an element \(i \in \{1,\dots,n\}\) such that \(i, \sigma(i), \sigma^2(i), \dots, \sigma^k(i)=i\) are the only elements moved by \(\sigma\). We’ll denote the cycle \(\sigma\) by \((s_0 \ s_1 \dots \ s_{k-1})\) where \(s_0=i, s_1=\sigma(i),\dots,s_{k-1}=\sigma^{k-1}(i)\).

Transposition

A transposition is a cycle of length \(2\). We denote below the transposition of elements \(a \neq b\) by \((a \ b)\) or \(\tau_{a,b}\).

We also recall some theorems on the symmetric group.

Theorem 1: The symmetric group \(\mathcal{S}_n\) is generated by its transpositions.
Proof.: We induct on \(n\). The theorem is trivial for \(n=2\). Now, suppose that \(\sigma\) is an element of \(\mathcal{S}_{n+1}\). We consider the permutation \(\sigma^\prime\) equal to \(\sigma\) if \(\sigma(n+1)=n+1\) and to \(\tau \circ \sigma\) if \(\sigma(n+1)=i \neq n+1\) where \(\tau\) is the transposition \((i \ n+1)\). In either case: \(\sigma^\prime(n+1)=n+1\). Let \(\mathcal{S}_{n+1}^\prime\) be the subgroup of elements of \(\mathcal{S}_{n+1}\) for which \(n+1\) is a fixed point. Evidently, \(\mathcal{S}_{n+1}^\prime\) is isomorphic to \(\mathcal{S}_n\) by restrictions of mappings. So by inductive hypothesis, \(\sigma^\prime\) is equal to a product of transpositions. And so is \(\sigma\) as \(\sigma = \sigma^\prime\) or \(\sigma=\tau \circ \sigma^\prime\). This concludes our proof by induction.

Theorem 2: The symmetric group \(\mathcal{S}_n\) is generated by the transpositions \((\tau_{i,i+1})_{1 \le i \le n-1}\).
Proof.: By theorem 1, it is enough to prove that any transposition \(\tau_{a,b}\) is generated by \((\tau_{i,i+1})_{1 \le i \le n-1}\). Without loss of generality, suppose \(a < b\). We induct on \(b-a \ge 1\). Our base case, \(b=a+1\) is trivial. For the inductive step, we note that: \[\tau_{a,b}=\tau_{a,a+1} \tau_{a+1,b} \tau_{a,a+1}\] Therefore if \(\tau_{a+1,b}\) is in the subgroup generated by \((\tau_{i,i+1})_{1 \le i \le n-1}\), it follows that \(\tau_{a,b}\) is, as well. Theorem 3: \(r=(1 \ 2)\) and \(s=(1 \ 2 \dots \ n)\) generate \(\mathcal{S}_n\).
Proof.: By theorem 2, this is a consequence of the relations: \(\tau_{i,i+1}=s^{i-1} \circ r \circ s^{-(i-1)}\) for \(1 \le i \le n-1\).

Returning to our initial question, we prove that when \(n\) is a prime number \(p\), then any transposition and any \(p\)-cycle generate \(\mathcal{S}_p\).
Proof.: Let
\[(a \ b \dots c \ d) \text{ and } (e \ f)\] be any \(p\)-cycle and any transposition. Any automorphism of \(\{1, \dots, p\}\) yields an automorphism of \(\mathcal{S}_p\) (more precisely an inner automorphism). Hence we can rename \(e=1\) such that the permutations are now:
\[(a^\prime \ b^\prime \dots 1 \dots c^\prime \ d^\prime)=(1 \dots c^\prime \ d^\prime \ a^\prime \ b^\prime \dots) \text{ and } (1 \ f^\prime)\] Now, for some \(1 \le k \le p-1\):
\[(1 \dots c^\prime \ d^\prime \ a^\prime \ b^\prime \dots)^k=(1 \ f^\prime \dots)\] and as \(p\) is supposed to be prime, \((1 \ f^\prime \dots)\) is a \(p\)-cycle. We can again rename the elements of \(\{1, \dots, p\}\) such that \(f^\prime = 2\) and the rest accordingly to get:
\[(1 \ 2 \dots p-1 \ p) \text{ and } (1 \ 2)\] for the \(p\)-cycle and the transposition that are our predefined generators. According to theorem 3, those permutations generate \(\mathcal{S}_n\).

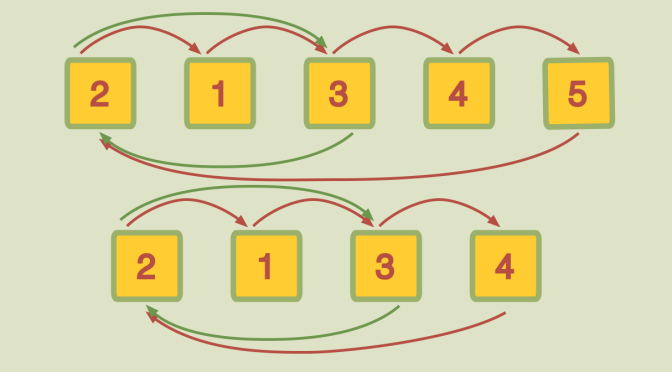
We finally show a counterexample. For instance \((1 \ 3)\) and \((1 \ 2 \ 3 \ 4)\) do not generate \(\mathcal{S}_4\). The reason is that these two permutations preserve congruences modulo \(2\) (if two numbers in \(\{1, 2, 3, 4\}\) are both even or both odd, applying either permutation to them returns values that are both even or both odd), so the subgroup they generate in \(\mathcal{S}_4\) has this property while \(\mathcal{S}_4\) does not: \(1,3\) are both odd, while their images by the transposition \((1 \ 2)\) have different parities.