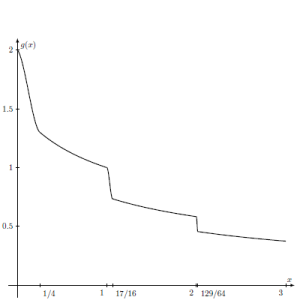
In that article, I gave examples of real valued functions defined on \((0,+\infty)\) that converge to zero and whose derivatives diverge. But those functions were not monotonic. Here I give an example of a decreasing real valued function \(g\) converging to zero at \(+\infty\) and whose derivative is unbounded.

We first consider the polynomial map:
\[P(x)=(1+2x)(1-x)^2=1-3x^2+2x^3\] on the segment \(I=[0,1]\). \(P\) derivative equals \(P^\prime(x)=-6x(1-x)\). Therefore \(P\) is decreasing on \(I\). Moreover we have \(P(0)=1\), \(P(1)=P^\prime(0)=P^\prime(1)=0\) and \(P^\prime(1/2)=-3/2\).

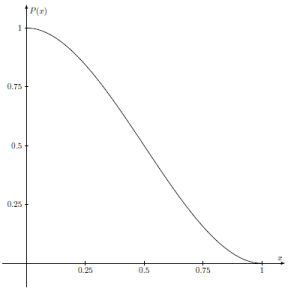
The intermediate function \(f: [0,+\infty) \rightarrow \mathbb{R}\) is defined piecewise as follow:
\[
f(x) =
\begin{cases}
\frac{1}{2^{n+1}} [1+P(4^{n+1}(x-n))] & \text{ for } x \in [n,n+\frac{1}{4^{n+1}})\\
\frac{1}{2^{n+1}} & \text{ for } x \in [n+\frac{1}{4^{n+1}},n+1)\\
\end{cases}
\] where \(n \in \mathbb{N}\).
For any \(n \in \mathbb{N}\), \(f\) is continuous on the segments \([n,n+\frac{1}{4^{n+1}})\) or \([n+\frac{1}{4^{n+1}},n+1)\). Considering right and left limits of \(f\) at points \(n\) and \(n+\frac{1}{4^{n+1}}\) for \(n \in \mathbb{N}\), one can prove that \(f\) is continuous on \([0,+\infty)\). Also \(f\) is non-increasing as \(f\) is non-increasing on each of its definition segments.

\(f\) is differentiable on all segments \((n+\frac{1}{4^{n+1}},n+1)\) where \(n \in \mathbb{N}\) as \(f\) is constant on those segments and hence \(f^\prime(x)=0\) there. \(f\) is also differentiable on all segments \((n,n+\frac{1}{4^{n+1}})\) as the composition of \(P\) which is differentiable on \((0,1)\) and a linear function. Let’s analyze the differentiability of \(f\) at points \(n \in \mathbb{N}\). For \(0 < h < 1/4^{n+1}\) we have \(\frac{f(n+h)-f(n)}{h}=\frac{P(4^{n+1}h)-1}{2^{n+1}h}=\frac{-3(4^{n+1})h+2(4^{n+1})^2h^2}{2^{n+1}}\). Therefore \(\lim\limits_{h \rightarrow 0^+}\frac{f(n+h)-f(n)}{h}=0\) proving that \(f\) is differentiable at \(n\) with \(f^\prime(n)=0\). Similarly the reader will prove that for \(n \in \mathbb{N}\), \(f\) is differentiable at \(n+\frac{1}{4^{n+1}}\) with again \(f^\prime(n+\frac{1}{4^{n+1}})=0\). Also, for \(x \in (n,n+\frac{1}{4^{n+1}})\) we have \(f^\prime(x)=2^{n+1}P^\prime(4^{n+1}(x-n))\). In particular for \(x=n+\frac{1}{2}\frac{1}{4^{n+1}}\) we have \(f^\prime(n+\frac{1}{2}\frac{1}{4^{n+1}})=-3\cdot2^n\) which proves that \(f^\prime\) is unbounded on \([0,+\infty)\). \(f\) is non-increasing but not decreasing. However it is easy to derive from \(f\) a decreasing function \(g\) that converges to \(0\) and whose derivative is unbounded... just consider \(g(x)=f(x)+1/{(x+1)}\).