According to Cauchy condensation test: for a non-negative, non-increasing sequence \((u_n)_{n \in \mathbb N}\) of real numbers, the series \(\sum_{n \in \mathbb N} u_n\) converges if and only if the condensed series \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) converges.
The test doesn’t hold for any non-negative sequence. Let’s have a look at counterexamples.
A sequence such that \(\sum_{n \in \mathbb N} u_n\) converges and \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges
Consider the sequence \[
u_n=\begin{cases}
\frac{1}{n} & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
0 & \text{ else} \end{cases}\] For \(n \in \mathbb N\) we have \[
0 \le \sum_{k = 1}^n u_k \le \sum_{k = 1}^{2^n} u_k = \sum_{k = 1}^{n} \frac{1}{2^k} < 1,\] therefore \(\sum_{n \in \mathbb N} u_n\) converges as its partial sums are positive and bounded above.
However \[\sum_{k=1}^n 2^k u_{2^k} = \sum_{k=1}^n 1 = n,\] so \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges.
A sequence such that \(\sum_{n \in \mathbb N} v_n\) diverges and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges
Consider the sequence \[
v_n=\begin{cases}
0 & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
\frac{1}{n} & \text{ else} \end{cases}\] We have \[
\sum_{k = 1}^{2^n} v_k = \sum_{k = 1}^{2^n} \frac{1}{k} – \sum_{k = 1}^{n} \frac{1}{2^k} > \sum_{k = 1}^{2^n} \frac{1}{k} -1\] which proves that the series \(\sum_{n \in \mathbb N} v_n\) diverges as the harmonic series is divergent. However for \(n \in \mathbb N\), \(2^n v_{2^n} = 0 \) and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges.

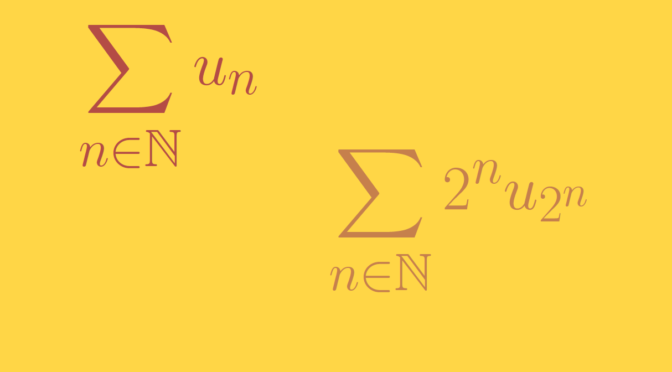
One thought on “Counterexamples around Cauchy condensation test”