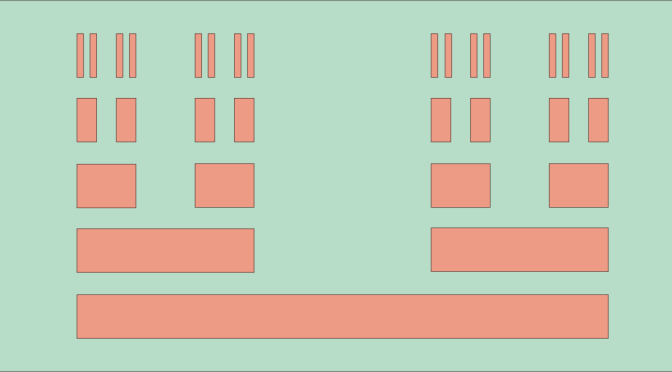
Definition of the Cantor set

The Cantor ternary set (named Cantor set below) \(K\) is a subset of the real segment \(I=[0,1]\). It is built by induction:

• Starting with \(K_0=I\)
• If \(K_n\) is a finite disjoint union of segments \(K_n=\cup_k \left[a_k,b_k\right]\), \[K_{n+1}=\bigcup_k \left(\left[a_k,a_k+\frac{b_k-a_k}{3}\right] \cup \left[a_k+2\frac{b_k-a_k}{3},b_k\right]\right)\]

And finally \(K=\displaystyle \bigcap_{n \in \mathbb{N}} K_n\). The Cantor set is created by repeatedly deleting the open middle third of a set of line segments starting with the segment \(I\).

The Cantor set is a closed set as it is an intersection of closed sets. Continue reading Cantor set: a null set having the cardinality of the continuum →