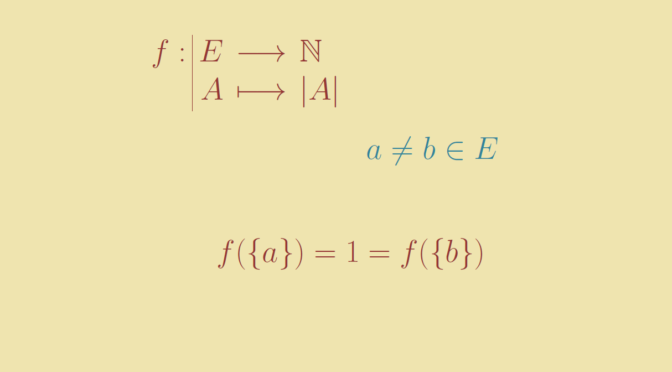Consider two partially ordered sets \((E,\le)\) and \((F,\le)\) and a strictly increasing map \(f : E \to F\). If the order \((E,\le)\) is total, then \(f\) is one-to-one. Indeed for distinct elements \(x,y \in E\), we have either \(x < y\) or \(y < x\) and consequently \(f(x) < f(y)\) or \(f(y) < f(x)\). Therefore \(f(x)\) and \(f(y)\) are different. This is not true anymore for a partial order \((E,\le)\). We give a counterexample.
Consider a finite set \(E\) having at least two elements and partially ordered by the inclusion. Let \(f\) be the map defined on the powerset \(\wp(E)\) that maps \(A \subseteq E\) to its cardinal \(\vert A \vert \). \(f\) is obviously strictly increasing. However \(f\) is not one-to-one as for distincts elements \(a,b \in E\) we have \[
f(\{a\}) = 1 = f(\{b\})\]