We’re looking here to relational expressions involving image and inverse image.
We consider a function \(f : X \to Y\) from the set \(X\) to the set \(Y\). If \(x\) is a member of \(X\), \(f(x)\) is the image of \(x\) under \(f\).
The image of a subset \(A \subset X\) under \(f\) is the subset (of \(Y\)) \[f(A)\stackrel{def}{=} \{f(x) : x \in A\}.\]
The inverse image of a subset \(B \subset Y\) is the subset of \(A\) \[f^{-1}(B)\stackrel{def}{=} \{x \in X : f(x) \in B\}.\] Important to understand is that here, \(f^{-1}\) is not the inverse function of \(f\).
We now look at relational expressions involving the image and the inverse image under \(f\).
Inverse images with unions and intersections
Following relations hold:
\[\begin{array}{c}
f^{-1}(B_1 \cup B_2) = f^{-1}(B_1) \cup f^{-1}(B_2)\\
f^{-1}(B_1 \cap B_2) = f^{-1}(B_1) \cap f^{-1}(B_2)
\end{array}\] Let’s prove the first equality as an example. We have \(x \in f^{-1}(B_1 \cup B_2)\) if and only if \(f(x) \in B_1 \cup B_2\) if and only if \(f(x) \in B_1\) or \(f(x) \in B_2\) which means exactly \(x \in f^{-1}(B_1) \cup f^{-1}(B_2)\).
Images with unions and intersections
Regarding images, we have following relations:
\[\begin{array}{c}
f(A_1 \cup A_2) = f(A_1) \cup f(A_2)\\
f(A_1 \cap A_2) \subset f(A_1) \cap f(A_2)
\end{array}\] You can observe that in the second relation, we only have an inclusion and it is on purpose. The equality \(f(A_1 \cap A_2) = f(A_1) \cap f(A_2)\) holds when \(f\) is one-to-one. Let’s prove that \(f(A_1) \cap f(A_2) \subset f(A_1 \cap A_2)\) in that case. \(y \in f(A_1) \cap f(A_2)\) means that \(y \in f(A_1)\) and \(y \in f(A_2)\). Therefore, there exist \(x_1 \in A_1\) and \(x_2 \in A_2\) such that \(y=f(x_1)=f(x_2)\). As \(f\) is supposed to be one-to-one, we must have \(x_1 = x_2 \in A_1 \cap A_2\). Consequently \(y=f(x_1)=f(x_2) \in f(A_1 \cap A_2)\) which allows us to conclude.
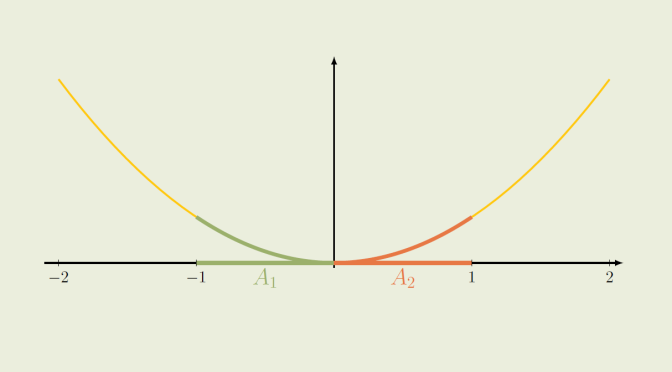
However, \(f(A_1 \cap A_2)\) can be a proper subset of \(f(A_1) \cap f(A_2)\) when \(f\) is not one-to-one and we provide a counterexample. Consider the real function \(f : x \mapsto x^2\) and the subsets \(A_1 = [-1,0] \subset \mathbb R\), \(A_2 = [0,1] \subset \mathbb R\). We have \[
\begin{array}{l}
A_1 \cap A_2 = \{0\} \text{ hence } f(A_1 \cap A_2) = \{0\} \\
f([-1,0]) = f([0,1])= [0,1] \text{ hence } f(A_1) \cap f(A_2) = [0,1]
\end{array}\] we finally get \(f(A_1 \cap A_2) \varsubsetneq f(A_1) \cap f(A_2)\) for that example.
About the inclusions \(f(f^{-1}(B)) \subset B\) and \(A \subset f^{-1}(f(A))\)
One can prove following inclusions:
\[\begin{array}{c}
f(f^{-1}(B)) \subset B\\
A \subset f^{-1}(f(A))
\end{array}\] The inclusion \(f(f^{-1}(B)) \subset B\) becomes an equality if \(f\) is onto as \(B \subset f(f^{-1}(B))\) in that case. For the prove, consider \(y \in B\). As \(f\) is supposed to be onto, it exists \(x \in X\) such that \(y=f(x)\), which means that \(x \in f^{-1}(B)\) and finally \(y=f(x) \in f(f^{-1}(B))\). If \(f\) is not onto, the inclusion \(f(f^{-1}(B)) \subset B\) can be proper. Let’s consider the \(\sin\) function and the subset \(B = [-1,2]\). As \(B\) contains the image of \(\sin\), namely \([-1,1]\), we have \(f^{-1}([-1,2]) = \mathbb R\) and \[[-1,1]=f(f^{-1}([-1,2]))=f(f^{-1}(B)) \varsubsetneq B = [-1,2]\]
For its part, the inclusion \(A \subset f^{-1}(f(A))\) becomes an equality if \(f\) is one-to-one. The proof is left to the reader. The inclusion can be proper if \(f\) is not one-to-one. Consider again the map \(f : x \mapsto x^2\) and \(A=[0,1]\). We have \(f(A)=f([0,1])=[0,1]\), \(f^{-1}(f(A)) = f^{-1}([0,1])=[-1,1]\) and finally \(A \varsubsetneq f^{-1}(f(A))\) as desired.