Most of Cauchy existence theorems for a differential equation
\begin{equation}
\textbf{x}^\prime = \textbf{f}(t,\textbf{x})
\end{equation} where \(t\) is a real variable and \(\textbf{x}\) a vector on a real vectorial space \(E\) are valid when \(E\) is of finite dimension or a Banach space. This is however not true for the Peano existence theorem.
Take for \(E\) the space of real sequences converging to \(0\) for the norm \(\Vert \textbf{x} \Vert = \sup_n \vert x_n \vert\). For all \(\textbf{x} \in E\) let’s note \(\textbf{y}=\textbf{f}(\textbf{x})\) the sequence \((y_n)\) defined by:
\begin{equation*}
y_n=\sqrt{\vert x_n \vert} + \frac{1}{n+1}
\end{equation*} As \(\lim\limits_{n \to +\infty} y_n=0\), \(\textbf{y}\) belongs to \(E\). As the real function \(\sqrt{\vert x \vert}\) is uniformly continuous on \(\mathbb{R}\), the function \(\textbf{y}=\textbf{f}(\textbf{x})\) is continuous on \(E\).
However, we’ll prove that the differential equation
\begin{equation}
\textbf{x}^\prime = \textbf{f}(\textbf{x})
\label{eq:eqglobal}
\end{equation} has no solution in \(E\) with initial condition \(\textbf{x}(0)=\textbf{0}\). If \(\textbf{u}\) was a solution, there would exist a sequence \(\textbf{u}(t)=[u_n(t)]\) of differentiable functions in a neighborhood of \(0\) satisfying:
\begin{equation}
u_n^\prime(t)=\sqrt{\vert u_n(t) \vert} + \frac{1}{n+1}
\label{eq:eqwithn}
\end{equation} and \(u_n(0)=0\) for all \(n \in \mathbb{N}\).
By direct integration it can be proved that each equation \eqref{eq:eqwithn} has a unique solution satisfying \(u_n(0)=0\). For all \(n \in \mathbb{N}\), \(u_n\) is an odd function defined on all \(\mathbb{R}\) and verifying for \(t \ge 0\): \(u_n(t) \ge \frac{t^2}{4}\). This last inequality, valid for all \(n \in \mathbb{N}\) contradicts the ability for \(\textbf{u}\) to belongs to \(E\). Therefore, the equation \eqref{eq:eqglobal} has no solution.
This counterexample is from the French mathematician Jean Dieudonné.

Dear Jean-Pierre Merx,
I done my calculations again and now I see that I was mistaken. Sorry for the trouble and thanks for providing the proof, now the inequality seems clear to me. 🙂
Best regards,
Tadashi
Dear Jean-Pierre Merx, congratulations for the wonderful site!
I wish success for the site and I’m looking forward for more counterexamples 🙂
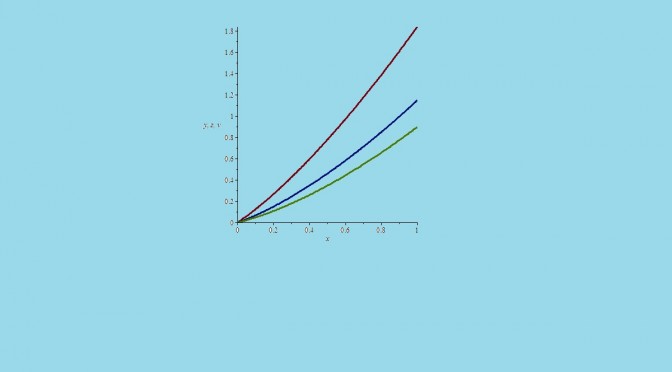
Between, I think there is a mistake in the last inequality of this counterexample, i.e. u_n(t) ≥ t ²/4 for t ≥ 0.
Consider for instance that n = 2. Then as the following plot suggests, there exists a q ≥ 0 such that the inequality is not valid for all t ≥ q.
Is there another way to prove that u doesn’t belongs to E?
Thanks a lot and best regards!
Dear Tadashi,
Thanks you very much for your encouragement! Indeed, I intend to publish more content. My target is at least a post per week, or more if I have more time.
In fact the inequality \(u_n(t) \ge \frac{t^2}{4}\) can be proven either by direction integration or by considering the inequality \(u_n^\prime(t) > \sqrt{u_n(t)}\) valid for all \(t>0\).
I have an issue to go to the link you provided. If you post it again, maybe I can have a look at it.
Thanks, Jean-Pierre.