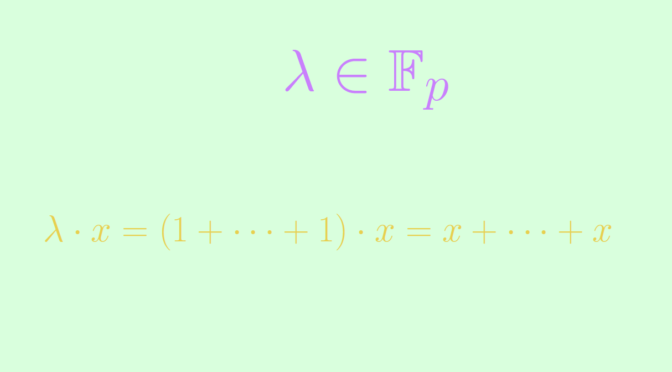Consider a vector space \(V\) over a field \(F\). A subspace \(W \subseteq V\) is an additive subgroup of \((V,+)\). The converse might not be true.
If the characteristic of the field is zero, then a subgroup \(W\) of \(V\) might not be an additive subgroup. For example \(\mathbb R\) is a vector space over \(\mathbb R\) itself. \(\mathbb Q\) is an additive subgroup of \(\mathbb R\). However \(\sqrt{2}= \sqrt{2}.1 \notin \mathbb Q\) proving that \(\mathbb Q\) is not a subspace of \(\mathbb R\).
Another example is \(\mathbb Q\) which is a vector space over itself. \(\mathbb Z\) is an additive subgroup of \(\mathbb Q\), which is not a subspace as \(\frac{1}{2} \notin \mathbb Z\).
Yet, an additive subgroup of a vector space over a prime field \(\mathbb F_p\) with \(p\) prime is a subspace. To prove it, consider an additive subgroup \(W\) of \((V,+)\) and \(x \in W\). For \(\lambda \in F\), we can write \(\lambda = \underbrace{1 + \dots + 1}_{\lambda \text{ times}}\). Consequently \[
\lambda \cdot x = (1 + \dots + 1) \cdot x= \underbrace{x + \dots + x}_{\lambda \text{ times}} \in W.\]
Finally an additive subgroup of a vector space over any finite field is not always a subspace. For a counterexample, take the non-prime finite field \(\mathbb F_{p^2}\) (also named \(\text{GF}(p^2)\)). \(\mathbb F_{p^2}\) is also a vector space over itself. The prime finite field \(\mathbb F_p \subset \mathbb F_{p^2}\) is an additive subgroup that is not a subspace of \(\mathbb F_{p^2}\).