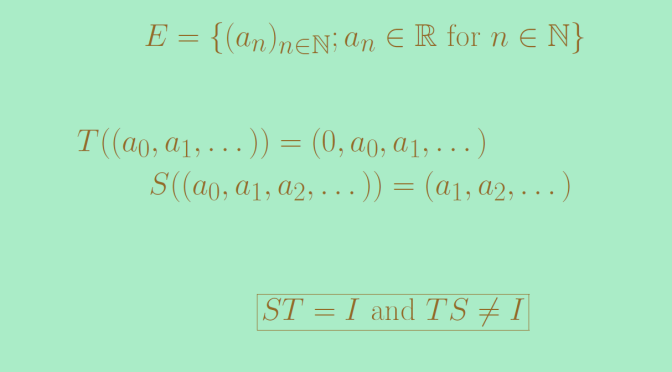We consider a vector space \(E\) and a linear map \(T \in \mathcal{L}(E)\) having a left inverse \(S\) which means that \(S \circ T = S T =I\) where \(I\) is the identity map in \(E\).

When \(E\) is of finite dimension, \(S\) is invertible.
For the proof we take \(x \in E\). We have \(S(T(x)) = I(x) = x\), which means that \(T(x)\) is a pre-image of \(x\) for \(S\) proving that \(S\) is onto. If \(E\) is supposed to be of finite dimension, \(S\) is also one-to-one and hence invertible and equal to \(T^{-1}\). Another way to prove that \(S\) is invertible is to use the determinant. We have \(\det(S T) = \det(S) \det(T)=\det(I)=1\), hence \(\det(S) \neq 0\) and \(S\) is invertible.

What about the case where \(E\) is of infinite dimension? In that case, a left inverse might not be a right inverse. We provide below a counterexample.

Consider the space \(E\) of real sequences, the linear mapping \(T\) that maps a sequence \((a_0,a_1, \dots)\) to the sequence \((0,a_0,a_1, \dots)\) and the linear mapping \(S\) that maps a sequence \((a_0,a_1,a_2, \dots)\) to the sequence \((a_1, a_2, \dots)\). It is clear that \(ST = I\). Now consider the sequence \(a=(1,0,0,0, \dots)\). We have \(S(a)=\textbf{0}\) where \(\textbf{0}\) is the sequence that vanishes identically and also \(T S(a) = \textbf{0}\) hence \(T S \neq I\).