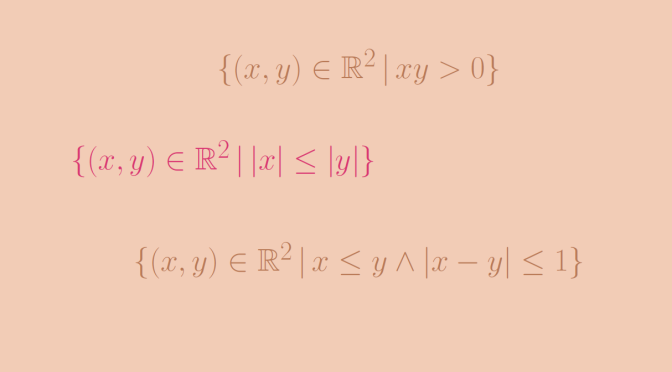We are considering here binary relations on a set \(A\). Let’s recall that a binary relation \(R\) on \(A\) is a subset of the cartesian product \(R \subseteq A \times A\). The statement \((x,y) \in R\) is read as \(x\) is \(R\)-related to \(y\) and also denoted by \(x R y \).

Some importants properties of a binary relation \(R\) are:

reflexive

For all \(x \in A\) it holds \(x R y\)

irreflexive

For all \(x \in A\) it holds not \(x R y\)

symmetric

For all \(x,y \in A\) it holds that if \(x R y\) then \(y R x\)

antisymmetric

For all \(x,y \in A\) if \(x R y\) and \(y R x\) then \(x=y\)

transitive

For all \(x,y,z \in A\) it holds that if \(x R y\) and \(y R z\) then \(x R z\)

A relation that is reflexive, symmetric and transitive is called an equivalence relation. Let’s see that being reflexive, symmetric and transitive are independent properties.

Symmetric and transitive but not reflexive

We provide two examples of such relations. For the first one, we take for \(A\) the set of the real numbers \(\mathbb R\) and the relation \[R = \{(x,y) \in \mathbb R^2 \, | \, xy >0\}.\] \(R\) is symmetric as the multiplication is also symmetric. \(R\) is also transitive as if \(xy > 0\) and \(yz > 0\) you get \(xy^2 z >0\). And as \(y^2 > 0\), we have \(xz > 0\) which means that \(x R z\). However, \(R\) is not reflexive as \(0 R 0\) doesn’t hold.

For our second example, we take \(A= \mathbb N\) and \(R=\{(1,1)\}\). It is easy to verify that \(R\) is symmetric and transitive. However \(R\) is not reflexive as \(n R n\) doesn’t hold for \(n \neq 1\).

Reflexive and transitive but not symmetric

We take \(A=\mathbb R\) and \[R = \{(x,y) \in \mathbb R^2 \, | \, \vert x \vert \le \vert y \vert\}.\] One can verify that \(R\) is reflexive and transitive. It is also not symmetric. It is not antisymmetric either. As a counterexample we have \(\vert -3 \vert \le \vert 3 \vert\) and \(\vert 3 \vert \le \vert -3 \vert\). However \(-3 \neq 3\).

Reflexive and symmetric but not transitive

Consider \(A=\mathbb R\) and \[R = \{(x,y) \in \mathbb R^2 \, | \, \vert x – y \vert \le 1\}.\] In other word, \(x\) is \(R\)-related to \(y\) if and only if the relative distance between \(x\) and \(y\) is less than \(1\) foot. \(R\) is reflexive and symmetric but not transitive as \(\vert 1 – 0 \vert \le 1\), \(\vert 2 – 1 \vert \le 1\) but \(\vert 2 – 0 \vert > 1\).

A relation that is reflexive, antisymmetric and transitive is called a partial order. Let’s see that being reflexive, antisymmetric and transitive are independent properties.

Reflexive and transitive but not antisymmetric

We already came across such a binary relation above considering \(A=\mathbb R\) and \[R = \{(x,y) \in \mathbb R^2 \, | \, \vert x \vert \le \vert y \vert\}.\]

Reflexive and antisymmetric but not transitive

Here we take \(A = \mathbb R\) and \[R = \{(x,y) \in \mathbb R^2 \, | \, x \le y \text{ and } \vert x-y \vert \le 1\}.\] \(R\) is reflexive and antisymmetric as \(\le\) is a partial order of \(\mathbb R\). \(R\) is not transitive as \(0 R 1\) and \(1 R 2\) while \(0 R 2\) doesn’t hold.

Antisymmetric and transitive but not reflexive

We define on \(\mathbb N\) the binary relation \(R\) by: \(a R b \) if and only if \(a\) is even and divides \(b\). If \(a R b\) and \(b R a\), \(a\) and \(b\) are both even and as the divisibility relation is antisymmetric, \(R\) is also antisymmetric. For \(a,b,c \in \mathbb N\), if \(aRb\) and \(b R c\) both hold, \(a,b\) are even and \(a\) divides \(c\) by transitivity of the divisibility relation. Hence \(a Rc\) which proves that \(R\) is transitive.

However, \(R\) is not reflexive as \(3 R 3\) doesn’t hold because \(3\) is not even.