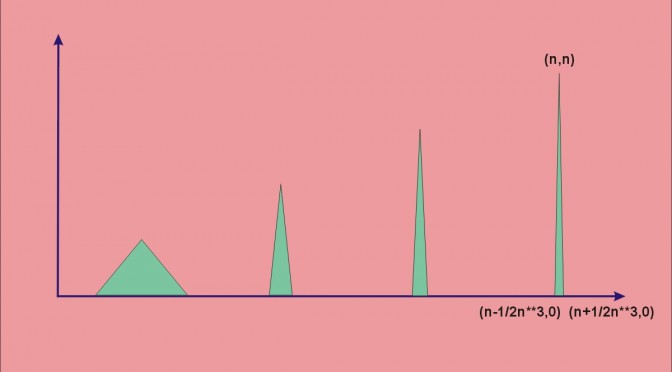
Consider the piecewise linear function \(f\) defined on \([0,+\infty)\) taking following values for all \(n \in \mathbb{N^*}\):
\[
f(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x=0\\
0 & \mbox{if } x=n-\frac{1}{2n^3}\\
n & \mbox{if } x=n\\
0 & \mbox{if } x=n+\frac{1}{2n^3}\\
\end{array}
\right.
\]
The graph of \(f\) can be visualized in the featured image of the post.
\(f\) is positive and continuous, unbounded as \(f(n)=n\) for all \(n \in \mathbb{N}\).
We now consider \(\int_0^{+\infty} f\). For \(X > 0\), we have:
\[\int_0^{X} f \le \int_0^{N + \frac{1}{2N^3}} f\]
where \(N=\lceil X \rceil\) and:
\[\int_0^{N + \frac{1}{2N^3}} f = \frac{1}{2}\sum_{n=1}^N \frac{1}{n^2}\]
as for all \(n \in \mathbb{N^*}\):
\[\int_{n – \frac{1}{2n^3}}^{n + \frac{1}{2n^3}} f = \frac{1}{2 n^2}\]
This proves that the integral of \(f\) is less than the sum of the convergent series \((\frac{1}{(n+1)^2})_{n \in \mathbb{N}}\). Therefore the integral converges.