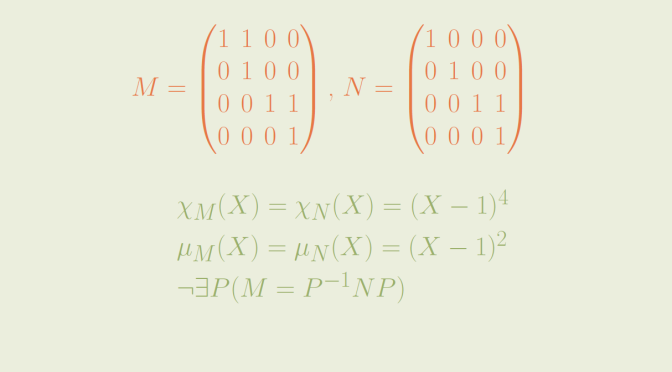Consider a square matrix \(A\) of dimension \(n \ge 1\) over a field \(\mathbb F\), i.e. \(A \in \mathcal M_n(\mathbb F)\). Results discuss below are true for any field \(\mathbb F\), in particular for \(\mathbb F = \mathbb R\) or \(\mathbb F = \mathbb C\).
A polynomial \(P \in \mathbb F[X]\) is called a vanishing polynomial for \(A\) if \(P(A) = 0\). If the matrix \(B\) is similar to \(B\) (which means that \(B=Q^{-1} A Q\) for some invertible matrix \(Q\)), and the polynomial \(P\) vanishes at \(A\) then \(P\) also vanishes at \(B\). This is easy to prove as we have \(P(B)=P(Q^{-1} A Q)=Q^{-1} P(A) Q\).
In particular, two similar matrices have the same minimal and characteristic polynomials.
Is the converse true? Are two matrices having the same minimal and characteristic polynomials similar?
The answer is negative as we’ll prove considering the matrices
\[M=\begin{pmatrix}
1 & 1 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{pmatrix} \text{ and }
N=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{pmatrix}\] written in the standard basis \((e_1,e_2,e_3,e_4)\).
As both matrices are triangular, the computation of the characteristic polynomials is easy and we get \[\chi_N(X)=\chi_M(X)=(X-1)^4\]
According to Cayley-Hamilton theorem, the minimal polynomials \(\mu_M(X)\) and \(\mu_N(X)\) of \(M\) and \(N\) respectively divide \((X-1)^4\). Those polynomials cannot be \(X-1\) as neither \(M\) nor \(N\) is equal to the identity matrix. However we have \(\mu_M(X)=\mu_N(X)=(X-1)^2\) as can be verified following an easy computation.
Another way to see it, is to notice that the restriction of \(M\) and \(N\) to supplementary subspaces \(U=\mathbf{span}(e_1,e_2)\) and \(V=\mathbf{span}(e_3,e_4)\) which are stable for both \(M\) and \(N\) are either
\[A=\begin{pmatrix}
1 & 1\\
0 & 1
\end{pmatrix} \text{ or }
B=\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}\] Then the polynomial \((X-1)^2\) is vanishing at \(A\) and \(B\) while the polynomial \(X-1\) is not vanishing at \(A\).
Finally, the matrices \(M\) and \(N\) are not similar. If that would be the case, the dimensions for \(M\) and \(N\) of the eigenspaces corresponding to the eigenvalue \(1\) would be equal. However we have \[\left\{
\begin{array}{lll}
\ker (M-I_4) = \mathbf{span}(e_1,e_3) & \text{ hence } & \dim \ker (M-I_4)=2\\
\ker (N-I_4) = \mathbf{span}(e_1,e_2,e_3) & \text{ hence } & \dim \ker (M-I_4)=3
\end{array}
\right. \]