We take a metric space \((E,d)\) and consider two closed subsets \(A,B\) having a distance \(d(A,B)\) equal to zero. We raise the following question: can \(A\) and \(B\) be disjoint – \(A \cap B=\emptyset\)?

If \(A\) or \(B\) is compact, let’s say \(A\), \(A \cap B\) cannot be empty. The proof is quite simple. As \(d(A,B) = 0\), for all \(n \in \mathbb{N}\) we can pick up \((a_n,b_n) \in A \times B\) with \(d(a_n,b_n) \le \frac{1}{n+1}\). As \(A\) is compact, we can find a subsequence of \((a_n)_{n \in \mathbb{N}}\) converging to a point \(a \in A\). Even if it means renumbering the subsequence, we can suppose that \(\lim\limits_{n \to +\infty} a_n = a\). As \(d(a,b_n) \le d(a,a_n)+d(a_n,b_n)\) and both terms of the right hand side of the inequality converge to zero, \((b_n)_{n \in \mathbb{N}}\) also converges to \(a\). As \(B\) is supposed to be closed, we have \(a \in B\) and finally \(a \in A \cap B\).

So we have to turn ourselves to the case where \(A\) and \(B\) are not compact to find a counterexample. If \(E = \mathbb{R}^n\) with \(n \ge 1\) that means \(A\) and \(B\) unbounded.

An example in the real line

Take \(A=\{a_n = n ; n \in \mathbb{N}\}\) and \(B=\{b_m = m + \frac{1}{m+2}; m \in \mathbb{N}\}\). \(A\) and \(B\) are disjoint as if \(n=m + \frac{1}{m+2}\) and \(n=m\) we get the contradiction \(\frac{1}{m+2}=0\) while if \(n \neq m\) we get the contradiction \(1 \le \vert n-m \vert = \frac{1}{m+2} <1\). However \(d(A,B) = 0\) because \(\lim\limits_{n \to +\infty} d(a_n-b_n) =0\).

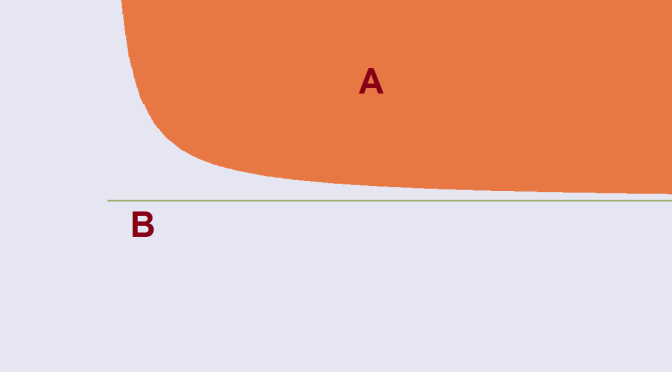
An example in the real plane

Take \(A=\{(x,y) ; y \ge 1/x > 0\}\) and \(B=\{(x,0) ; x \ge 0\}\).
\(A\) and \(B\) are closed subsets of the real plane and their intersection is empty. The proof is left to the reader.