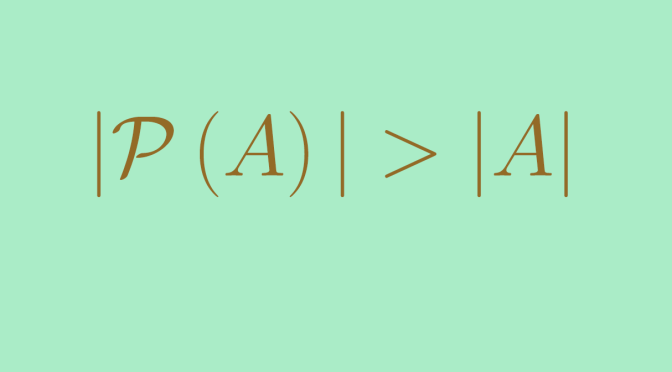We have seen in this article several sets that are infinite and countable. Namely, the set of natural numbers \(\mathbb N\), the set of integers \(\mathbb Z\), the set of rational numbers \(\mathbb Q\). We have seen that the product \(\mathbb N \times \mathbb N\) is also countable. The question then arises, “Are all infinite sets countable?”.
The answer is negative and we prove that \(\mathbb R\) is not countable.
The set of all reals \(\mathbb R\) is not countable
Suppose for the sake of contradiction that \(\mathbb R\) is countable and that \(\mathbb R = \{x_n \ | \ n \in \mathbb N\}\), the \(x_n\) being all distinct. We build by induction two sequences \((a_n)_{n \in \mathbb N}\) increasing and \((b_n)_{n \in \mathbb N}\) decreasing such that:
- \(a_n < b_n\) for all \(n \in \mathbb N\),
- \(\vert a_n – b_n \vert \) converges to zero,
- and \(x_n \notin [a_{n+1},b_{n+1}]\).
Let’s start with \(a_0 = 0\) and \(b_0 = 1\) and assume that we have built \(a_0, \dots, a_n\) and \(b_0, \dots, b_n\) satisfying above properties. If \(x_n \notin (a_n,b_n)\) we take \[
a_{n+1}=a_n+\frac{b_n-a_n}{4}, \, b_{n+1}=b_n-\frac{b_n-a_n}{4}\] while if \(x_n \in (a_n,b_n)\) we take \[
a_{n+1}=a_n+\frac{x_n-a_n}{4}, \, b_{n+1}=x_n-\frac{x_n-a_n}{4}\] One can verify that \(a_n < a_{n+1}\), \(b_{n+1} < b_n\), \(a_{n+1} < b_{n+1}\), \(\vert a_{n+1} - b_{n+1}\vert \le \frac{\vert a_n - b_n \vert}{2}\) and \(x_n \notin [a_{n+1},b_{n+1}]\). The induction step is complete.
Considering the properties of \((a_n)\) and \((b_n)\), those two sequences converge to a real number that we denote by \(\lambda\). By hypothesis, there exists \(N \in \mathbb N\) such that \(\lambda = x_N\). We also have \(a_{N+1} < \lambda < b_{N+1}\) in contradiction with \(x_N \notin [a_{N+1},b_{N+1}]\). Finally, \(\mathbb R\) cannot be countable.
Cantor’s theorem
So, the cardinality of \(\mathbb R\) is greater than the one of \(\mathbb N\). Can one find a set with a cardinal greater than the one of \(\mathbb R\)? The answer is positive. More generally, Cantor’s theorem states that, for any set \(A\), the set of all subsets of \(A\) (the power set of \(A\)) has a strictly greater cardinality than \(A\) itself. For the proof of Cantor’s theorem, suppose that \(f\) is a surjection from \(A\) onto the power set of \(A\), \(\mathcal P \left({A}\right)\) and consider \[B = \{x \in A \ | \ x \notin f(x)\}\] By hypothesis, there exists \(y \in A\) such that \(B=f(y)\). We then have the contradiction \[y \in B \Leftrightarrow y \notin f(y) \Leftrightarrow y \notin B\] Hence \(\mathcal P \left({A}\right)\) has a cardinality strictly greater than \(A\).
There is no greatest cardinal.