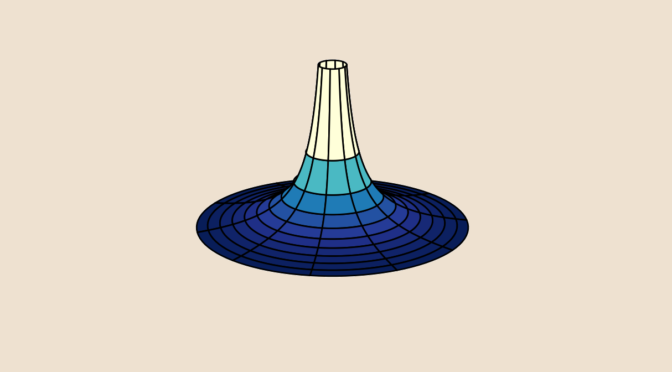
Can you paint a surface with infinite area with a finite quantity of paint? For sure… let’s do it!
Consider the 3D surface given in cylindrical coordinates as \[
S(\rho,\varphi):\begin{cases}
x &= \rho \cos \varphi\\
y &= \rho \sin \varphi\\
z &= \frac{1}{\rho}\end{cases}\] for \((\rho,\varphi) \in [1,\infty) \times [0, 2 \pi)\). The surface is named Gabriel’s horn.
Volume of Gabriel’s horn
The volume of Gabriel’s horn is \[
V = \pi \int_1^\infty \left( \frac{1}{\rho^2} \right) \ d\rho = \pi\] which is finite.
Area of Gabriel’s horn
The area of Gabriel’s horn for \((\rho,\varphi) \in [1,a) \times [0, 2 \pi)\) with \(a > 1\) is: \[
A = 2 \pi \int_1^a \frac{1}{\rho} \sqrt{1+\left( -\frac{1}{\rho^2} \right)^2} \ d\rho \ge 2 \pi \int_1^a \frac{d \rho}{\rho} = 2 \pi \log a.\] As the right hand side of inequality above diverges to \(\infty\) as \(a \to \infty\), we can conclude that the area of Gabriel’s horn is infinite.
Conclusion
Gabriel’s horn could be filled with a finite quantity of paint… therefore painting a surface with infinite area. Unfortunately the thickness of the paint coat is converging to \(0\) as \(z\) goes to \(\infty\), leading to a paint which won’t be too visible!