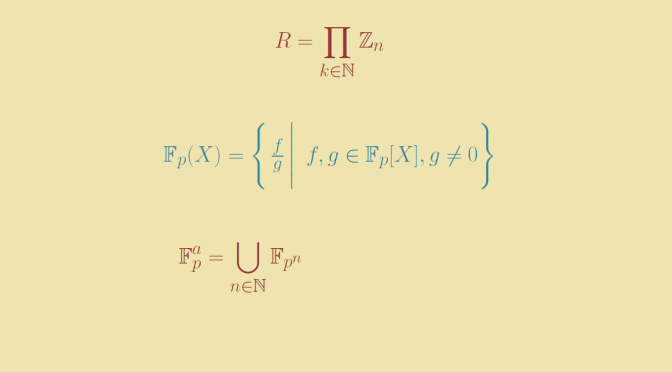Familiar to us are infinite fields whose characteristic is equal to zero like $\mathbb Z, \mathbb Q, \mathbb R$ or the field of constructible numbers.

We’re also familiar with rings having infinite number of elements and zero for characteristic like:

• The rings of polynomials $\mathbb Z[X], \mathbb Q[X], \mathbb R[X]$.
• The rings of matrices $\mathcal{M}_2(\mathbb R)$.
• Or the ring of real continuous functions defined on $\mathbb R$.

We also know rings or fields like integers modulo $n$ (with $n \ge 2$) $\mathbb Z_n$ or the finite field $\mathbb F_q$ with $q=p^r$ elements where $p$ is a prime.

We provide below examples of infinite rings or fields with positive characteristic.

Infinite rings with positive characteristic

Consider the ring $\mathbb Z_n[X]$ of polynomials in one variable $X$ with coefficients in $\mathbb Z_n$ for $n \ge 2$ integer. It is an infinite ring since $\mathbb X^m \in \mathbb{Z}_n[X]$ for all positive integers $m$, and $X^r \neq X^s$ for $r \neq s$. But the characteristic of $\mathbb Z_n[X]$ is clearly $n$.

Another example is based on product of rings. If $I$ is an index set and $(R_i)_{i \in I}$ a family of rings, one can define the product ring $\displaystyle \prod_{i \in I} R_i$. The operations are defined the natural way with $(a_i)_{i \in I} + (b_i)_{i \in I} = (a_i+b_i)_{i \in I}$ and $(a_i)_{i \in I} \cdot (b_i)_{i \in I} = (a_i \cdot b_i)_{i \in I}$. Fixing $n \ge 2$ integer and taking $I = \mathbb N$, $R_i = \mathbb Z_n$ for all $i \in I$ we get the ring $\displaystyle R = \prod_{k \in \mathbb N} \mathbb Z_n$. $R$ multiplicative identity is the sequence with all terms equal to $1$. The characteristic of $R$ is $n$ and $R$ is obviously infinite. Continue reading Infinite rings and fields with positive characteristic →