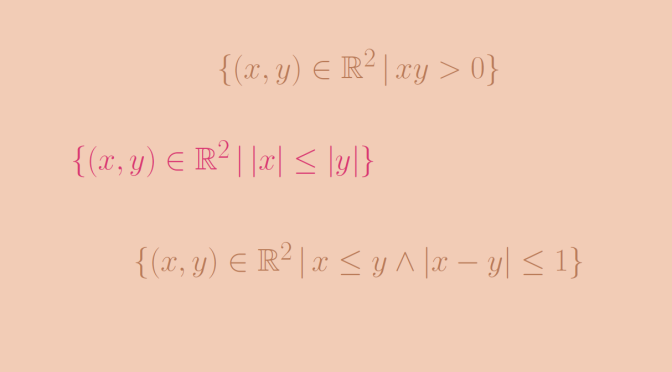We are considering here binary relations on a set \(A\). Let’s recall that a binary relation \(R\) on \(A\) is a subset of the cartesian product \(R \subseteq A \times A\). The statement \((x,y) \in R\) is read as \(x\) is \(R\)-related to \(y\) and also denoted by \(x R y \).

Some importants properties of a binary relation \(R\) are:

reflexive

For all \(x \in A\) it holds \(x R y\)

irreflexive

For all \(x \in A\) it holds not \(x R y\)

symmetric

For all \(x,y \in A\) it holds that if \(x R y\) then \(y R x\)

antisymmetric

For all \(x,y \in A\) if \(x R y\) and \(y R x\) then \(x=y\)

transitive

For all \(x,y,z \in A\) it holds that if \(x R y\) and \(y R z\) then \(x R z\)

A relation that is reflexive, symmetric and transitive is called an equivalence relation. Let’s see that being reflexive, symmetric and transitive are independent properties.

Symmetric and transitive but not reflexive

We provide two examples of such relations. For the first one, we take for \(A\) the set of the real numbers \(\mathbb R\) and the relation \[R = \{(x,y) \in \mathbb R^2 \, | \, xy >0\}.\] \(R\) is symmetric as the multiplication is also symmetric. \(R\) is also transitive as if \(xy > 0\) and \(yz > 0\) you get \(xy^2 z >0\). And as \(y^2 > 0\), we have \(xz > 0\) which means that \(x R z\). However, \(R\) is not reflexive as \(0 R 0\) doesn’t hold.

For our second example, we take \(A= \mathbb N\) and \(R=\{(1,1)\}\). It is easy to verify that \(R\) is symmetric and transitive. However \(R\) is not reflexive as \(n R n\) doesn’t hold for \(n \neq 1\). Continue reading Around binary relations on sets →