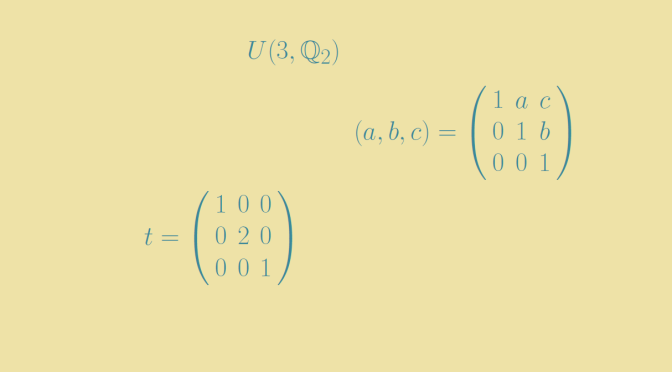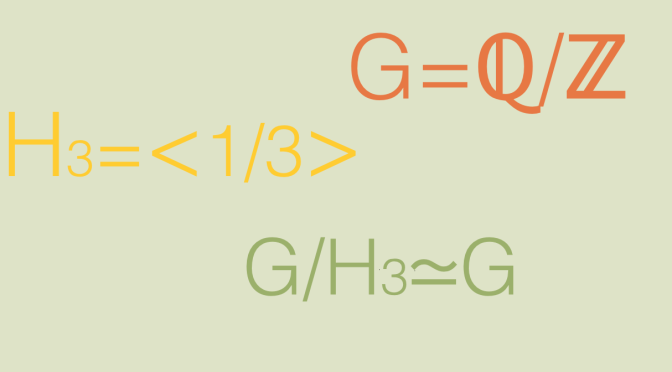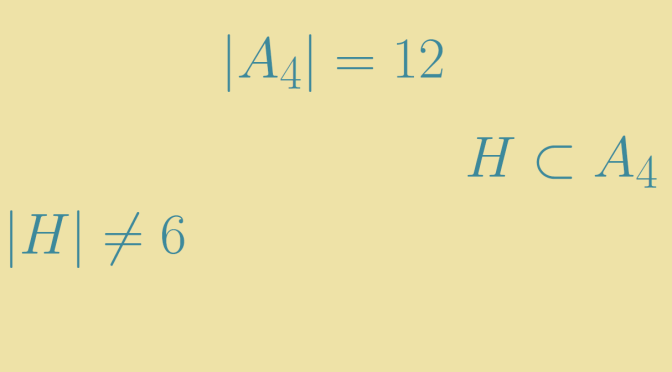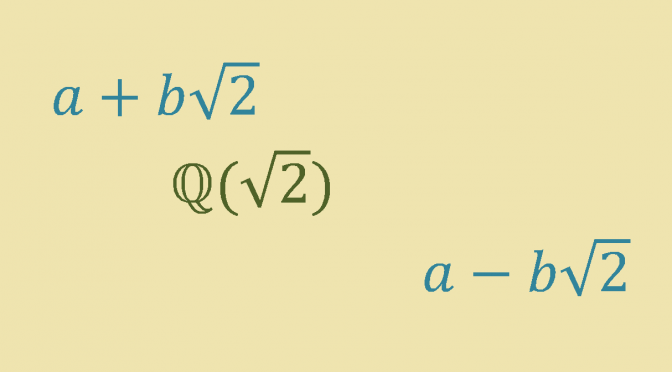Let \(\mathbb{Q}_2\) be the ring of rational numbers of the form \(m2^n\) with \(m, n \in \mathbb{Z}\) and \(N = U(3, \mathbb{Q}_2)\) the group of unitriangular matrices of dimension \(3\) over \(\mathbb{Q}_2\). Let \(t\) be the diagonal matrix with diagonal entries: \(1, 2, 1\) and put \(H = \langle t, N \rangle\). We will prove that \(H\) is finitely generated and that one of its quotient group \(G\) is isomorphic to a proper quotient group of \(G\). Continue reading A finitely generated soluble group isomorphic to a proper quotient group
Tag Archives: algebra
A (not finitely generated) group isomorphic to a proper quotient group
The basic question that we raise here is the following one: given a group \(G\) and a proper subgroup \(H\) (i.e. \(H \notin \{\{1\},G\}\), can \(G/H\) be isomorphic to \(G\)? A group \(G\) is said to be hopfian (after Heinz Hopf) if it is not isomorphic with a proper quotient group.
All finite groups are hopfian as \(|G/H| = |G| \div |H|\). Also, all simple groups are hopfian as a simple group doesn’t have proper subgroups.
So we need to turn ourselves to infinite groups to uncover non hopfian groups. Continue reading A (not finitely generated) group isomorphic to a proper quotient group
Converse of Lagrange’s theorem does not hold
Lagrange’s theorem, states that for any finite group \(G\), the order (number of elements) of every subgroup \(H\) of \(G\) divides the order of \(G\) (denoted by \(\vert G \vert\)).
Lagrange’s theorem raises the converse question as to whether every divisor \(d\) of the order of a group is the order of some subgroup. According to Cauchy’s theorem this is true when \(d\) is a prime.
However, this does not hold in general: given a finite group \(G\) and a divisor \(d\) of \(\vert G \vert\), there does not necessarily exist a subgroup of \(G\) with order \(d\). The alternating group \(G = A_4\), which has \(12\) elements has no subgroup of order \(6\). We prove it below. Continue reading Converse of Lagrange’s theorem does not hold
A field that can be ordered in two distinct ways
For a short reminder about ordered fields you can have a look to following post. We prove there that \(\mathbb{Q}\) can be ordered in only one way.
That is also the case of \(\mathbb{R}\) as \(\mathbb{R}\) is a real-closed field. And one can prove that the only possible positive cone of a real-closed field is the subset of squares.
However \(\mathbb{Q}(\sqrt{2})\) is a subfield of \(\mathbb{R}\) that can be ordered in two distinct ways. Continue reading A field that can be ordered in two distinct ways
An infinite field that cannot be ordered
Introduction to ordered fields
Let \(K\) be a field. An ordering of \(K\) is a subset \(P\) of \(K\) having the following properties:
- ORD 1
- Given \(x \in K\), we have either \(x \in P\), or \(x=0\), or \(-x \in P\), and these three possibilities are mutually exclusive. In other words, \(K\) is the disjoint union of \(P\), \(\{0\}\), and \(-P\).
- ORD 2
- If \(x, y \in P\), then \(x+y\) and \(xy \in P\).
We shall also say that \(K\) is ordered by \(P\), and we call \(P\) the set of positive elements. Continue reading An infinite field that cannot be ordered