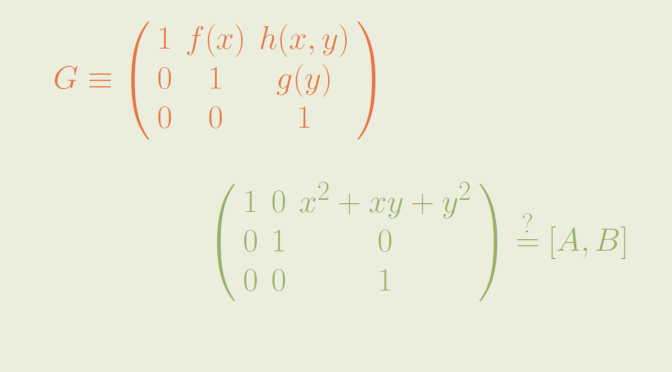We give here an example of a division ring which is not commutative. According to Wedderburn theorem every finite division ring is commutative. So we must turn to infinite division rings to find a non-commutative one, i.e. a skew field.
Let’s introduce the skew field of the Hamilton’s quaternions \[\mathbb H = \left\{\begin{pmatrix}
u & -\overline{v} \\
v & \overline{u}
\end{pmatrix} \ | \ u,v \in \mathbb C\right\}\] Continue reading The skew field of Hamilton’s quaternions
We study some properties of the Prüfer \(p\)-group \(\mathbb{Z}_{p^\infty}\) for a prime number \(p\). The Prüfer \(p\)-group may be identified with the subgroup of the circle group, consisting of all \(p^n\)-th roots of unity as \(n\) ranges over all non-negative integers:
\[\mathbb{Z}_{p^\infty}=\bigcup_{k=0}^\infty \mathbb{Z}_{p^k} \text{ where } \mathbb{Z}_{p^k}= \{e^{\frac{2 i \pi m}{p^k}} \ | \ 0 \le m \le p^k-1\}\]
First, let’s notice that for \(0 \le m \le n\) integers we have \(\mathbb{Z}_{p^m} \subseteq \mathbb{Z}_{p^n}\) as \(p^m | p^n\). Also for \(m \ge 0\) \(\mathbb{Z}_{p^m}\) is a subgroup of the circle group. We also notice that all elements of \(\mathbb{Z}_{p^\infty}\) have finite orders which are powers of \(p\). Continue reading An infinite group whose proper subgroups are all finite
I here provide a simple example of a group whose set of commutators is not a subgroup. The counterexample is due to P.J. Cassidy (1979).
Let \(k[x,y]\) denote the ring of all polynomials in two variables over a field \(k\), and let \(k[x]\) and \(k[y]\) denote the subrings of all polynomials in \(x\) and in \(y\) respectively. \(G\) is the set of all upper unitriangular matrices of the form
\[A=\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)\] where \(f(x) \in k[x]\), \(g(y) \in k[y]\), and \(h(x,y) \in k[x,y]\). The matrix \(A\) will also be denoted \((f,g,h)\).
Let’s verify that \(G\) is a group. The products of two elements \((f,g,h)\) and \((f^\prime,g^\prime,h^\prime)\) is
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc}
1 & f^\prime(x) & h^\prime(x,y) \\
0 & 1 & g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\]
\[=\left(\begin{array}{ccc}
1 & f(x)+f^\prime(x) & h(x,y)+h^\prime(x,y)+f(x)g^\prime(y) \\
0 & 1 & g(y)+g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\] which is an element of \(G\). We also have:
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)^{-1} =
\left(\begin{array}{ccc}
1 & -f(x) & f(x)g(y) – h(x,y) \\
0 & 1 & -g(y) \\
0 & 0 & 1 \end{array}\right)\] proving that the inverse of an element of \(G\) is also an element of \(G\). Continue reading The set of all commutators in a group need not be a subgroup
Can the symmetric group \(\mathcal{S}_n\) be generated by any transposition and any \(n\)-cycle for \(n \ge 2\) integer? is the question we deal with.
We first recall some terminology:
Continue reading Generating the symmetric group with a transposition and a maximal length cycle
In this article, we consider a group \(G\) and two subgroups \(H\) and \(K\). Let \(HK=\{hk \text{ | } h \in H, k \in K\}\).
\(HK\) is a subgroup of \(G\) if and only if \(HK=KH\). For the proof we first notice that if \(HK\) is a subgroup of \(G\) then it’s closed under inverses so \(HK = (HK)^{-1} = K^{-1}H^{-1} = KH\). Conversely if \(HK = KH\) then take \(hk\), \(h^\prime k^\prime \in HK\). Then \((hk)(h^\prime k^\prime)^{-1} = hk(k^\prime)^{-1}(h^\prime)^{-1}\). Since \(HK = KH\) we can rewrite \(k(k^\prime)^{-1}(h^\prime)^{-1}\) as \(h^{\prime \prime}k^{\prime \prime}\) for some new \(h^{\prime \prime} \in H\), \(k^{\prime \prime} \in K\). So \((hk)(h^\prime k^\prime)^{-1}=hh^{\prime \prime}k^{\prime \prime}\) which is in \(HK\). This verifies that \(HK\) is a subgroup. Continue reading Two subgroups whose product is not a subgroup
Let us recall that a square matrix \(A\) is called diagonalizable if it is similar to a diagonal matrix, i.e. if there exists an invertible matrix \(P\) such that \(P^{-1}AP\) is a diagonal matrix. Continue reading A diagonalizable matrix over Q but not over Z
We consider a vector space \(V\) of dimension \(2\) over a field \(\mathbb{K}\). The matrix:
\[A=\left( \begin{array}{cc}
0 & 1 \\
0 & 0 \end{array} \right)\] has several wonderful properties!
Zero is the only eigenvalue. The corresponding characteristic space is \(\mathbb{K} . e_1\) where \((e_1,e_2)\) is the standard basis. The minimal polynomial of \(A\) is \(\mu_A(X)=X^2\). Continue reading One matrix having several interesting properties
Let’s consider a polynomial of degree \(q \ge 1\) over a field \(K\). It is well known that the sum of the multiplicities of the roots of \(P\) is less or equal to \(q\).
The result remains for polynomials over an integral domain. What is happening for polynomials over a commutative ring? Continue reading On polynomials having more roots than their degree
We raise here the following question: “can a vector space \(E\) be written as a finite union of proper subspaces”?
Let’s consider the simplest case, i.e. writing \(E= V_1 \cup V_2\) as a union of two proper subspaces. By hypothesis, one can find two non-zero vectors \(v_1,v_2\) belonging respectively to \(V_1 \setminus V_2\) and \(V_2 \setminus V_1\). The relation \(v_1+v_2 \in V_1\) leads to the contradiction \(v_2 = (v_1+v_2)-v_1 \in V_1\) while supposing \(v_1+v_2 \in V_2\) leads to the contradiction \(v_1 = (v_1+v_2)-v_2 \in V_2\). Therefore, a vector space can never be written as a union of two proper subspaces.
We now analyze if a vector space can be written as a union of \(n \ge 3\) proper subspaces. We’ll see that it is impossible when \(E\) is a vector space over an infinite field. But we’ll describe a counterexample of a vector space over the finite field \(\mathbb{Z}_2\) written as a union of three proper subspaces. Continue reading A vector space written as a finite union of proper subspaces
We consider a vector space \(E\) and a linear map \(T \in \mathcal{L}(E)\) having a left inverse \(S\) which means that \(S \circ T = S T =I\) where \(I\) is the identity map in \(E\).
When \(E\) is of finite dimension, \(S\) is invertible. Continue reading A linear map having a left inverse which is not a right inverse
