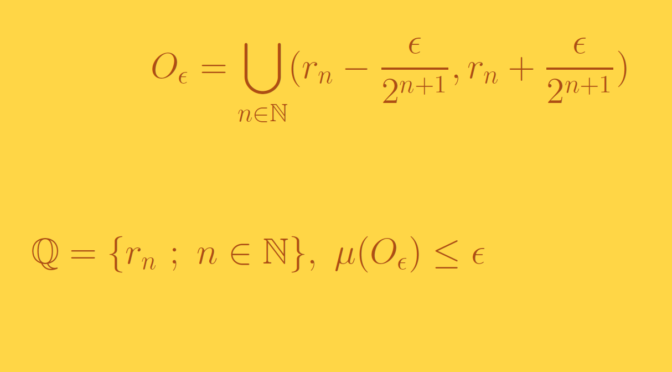The set \(\mathbb Q\) of the rational number is countable infinite and dense in \(\mathbb R\). You can have a look here on a way to build a bijective map between \(\mathbb N\) and \(\mathbb Q\).

Now given \(\epsilon > 0\), can one find an open set \(O_\epsilon\) of measure less than \(\epsilon\) with \(\mathbb Q \subseteq O_\epsilon\)?

The answer is positive. Let’s denote \[
O_\epsilon = \bigcup_{n \in \mathbb N} (r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\] where \((r_n)_{n \in \mathbb N}\) is an enumeration of the rationals. Obviously \(\mathbb Q \subseteq O_\epsilon\). Using countable subadditivity of Lebesgue measure \(\mu\), we get:
\begin{align*}
\mu(O_\epsilon) &\le \sum_{n \in \mathbb N} \mu((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}}))\\
&= \sum_{n \in \mathbb N} \frac{2 \epsilon}{2^{n+1}} = \sum_{n \in \mathbb N} \frac{\epsilon}{2^n} = \epsilon
\end{align*}

Therefore we’re done. Some additional comments:

• While Lebesgue measure of the reals is infinite and the rationals are dense in the reals, we can include the rationals in an open set of measure as small as desired!
• The open segments \((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\) are overlapping. Hence \(\mu(O_\epsilon)\) is strictly less than \(\epsilon\).