The ratio test is a test for the convergence of a series \[
\sum_{n=1}^\infty a_n \] where each term is a real or complex number and is nonzero when \(n\) is large. The test is sometimes known as d’Alembert’s ratio test.
Suppose that \[\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert = l\] The ratio test states that:
- if \(l < 1\) then the series converges absolutely;
- if \(l > 1\) then the series diverges.
What if \(l = 1\)? One cannot conclude in that case.
Cases where \(l=1\) and the series diverges
Consider the harmonic series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n}\). We have \(\lim\limits_{n \to \infty} \frac{n+1}{n} = 1\). It is well know that the harmonic series diverges. Recall that one proof uses the Cauchy’s convergence test based for \(k \ge 1\) on the inequalities: \[
\sum_{n=2^k+1}^{2^{k+1}} \frac{1}{n} \ge \sum_{n=2^k+1}^{2^{k+1}} \frac{1}{2^{k+1}} = \frac{2^{k+1}-2^k}{2^{k+1}} \ge \frac{1}{2}\]
An even simpler case is the series \(\displaystyle \sum_{n=1}^\infty 1\).
Cases where \(l=1\) and the series converges
We also have \(\lim\limits_{n \to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert = 1\) for the infinite series \(\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}\). The series is however convergent as for \(n \ge 1\) we have:\[
0 \le \frac{1}{(n+1)^2} \le \frac{1}{n(n+1)} = \frac{1}{n} – \frac{1}{n+1}\] and the series \(\displaystyle \sum_{n=1}^\infty \left(\frac{1}{n} – \frac{1}{n+1} \right)\) obviously converges.
Another example is the alternating series \(\displaystyle \sum_{n=1}^\infty \frac{(-1)^n}{n}\).

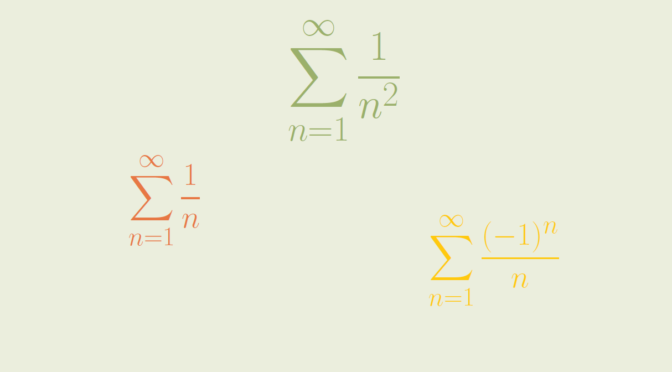
One thought on “Ratio test”