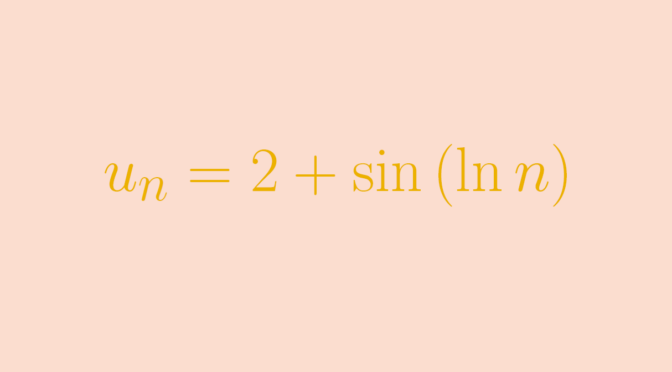Analysis

Counterexamples on real sequences (part 3)

Leave a comment

This article is a follow-up of Counterexamples on real sequences (part 2).

Let \((u_n)\) be a sequence of real numbers.

If \(u_{2n}-u_n \le \frac{1}{n}\) then \((u_n)\) converges?

This is wrong. The sequence
\[u_n=\begin{cases} 0 & \text{for } n \notin \{2^k \ ; \ k \in \mathbb N\}\\
1- 2^{-k} & \text{for } n= 2^k\end{cases}\]
is a counterexample. For \(n \gt 2\) and \(n \notin \{2^k \ ; \ k \in \mathbb N\}\) we also have \(2n \notin \{2^k \ ; \ k \in \mathbb N\}\), hence \(u_{2n}-u_n=0\). For \(n = 2^k\) \[
0 \le u_{2^{k+1}}-u_{2^k}=2^{-k}-2^{-k-1} \le 2^{-k} = \frac{1}{n}\] and \(\lim\limits_{k \to \infty} u_{2^k} = 1\). \((u_n)\) does not converge as \(0\) and \(1\) are limit points.

If \(\lim\limits_{n} \frac{u_{n+1}}{u_n} =1\) then \((u_n)\) has a finite or infinite limit?

This is not true. Let’s consider the sequence
\[u_n=2+\sin(\ln n)\] Using the inequality \(
\vert \sin p – \sin q \vert \le \vert p – q \vert\)
which is a consequence of the mean value theorem, we get \[
\vert u_{n+1} – u_n \vert = \vert \sin(\ln (n+1)) – \sin(\ln n) \vert \le \vert \ln(n+1) – \ln(n) \vert\] Therefore \(\lim\limits_n \left(u_{n+1}-u_n \right) =0\) as \(\lim\limits_n \left(\ln(n+1) – \ln(n)\right) = 0\). And \(\lim\limits_{n} \frac{u_{n+1}}{u_n} =1\) because \(u_n \ge 1\) for all \(n \in \mathbb N\).

I now assert that the interval \([1,3]\) is the set of limit points of \((u_n)\). For the proof, it is sufficient to prove that \([-1,1]\) is the set of limit points of the sequence \(v_n=\sin(\ln n)\). For \(y \in [-1,1]\), we can pickup \(x \in \mathbb R\) such that \(\sin x =y\). Let \(\epsilon > 0\) and \(M \in \mathbb N\) , we can find an integer \(N \ge M\) such that \(0 < \ln(n+1) - \ln(n) \lt \epsilon\) for \(n \ge N\). Select \(k \in \mathbb N\) with \(x +2k\pi \gt \ln N\) and \(N_\epsilon\) with \(\ln N_\epsilon \in (x +2k\pi, x +2k\pi + \epsilon)\). This is possible as \((\ln n)_{n \in \mathbb N}\) is an increasing sequence and the length of the interval \((x +2k\pi, x +2k\pi + \epsilon)\) is equal to \(\epsilon\). We finally get \[ \vert u_{N_\epsilon} - y \vert = \vert \sin \left(\ln N_\epsilon \right) - \sin \left(x + 2k \pi \right) \vert \le \left(\ln N_\epsilon - (x +2k\pi)\right) \le \epsilon\] proving that \(y\) is a limit point of \((u_n)\).

Algebra

A Commutative Ring with Infinitely Many Units

Leave a comment

In a ring \(R\) a unit is any element \(u\) that has a multiplicative inverse \(v\), i.e. an element \(v\) such that \[
uv=vu=1,\] where \(1\) is the multiplicative identity.

The only units of the commutative ring \(\mathbb Z\) are \(-1\) and \(1\). For a field \(\mathbb F\) the units of the ring \(\mathrm M_n(\mathbb F)\) of the square matrices of dimension \(n \times n\) is the general linear group \(\mathrm{GL}_n(\mathbb F)\) of the invertible matrices. The group \(\mathrm{GL}_n(\mathbb F)\) is infinite if \(\mathbb F\) is infinite, but the ring \(\mathrm M_n(\mathbb F)\) is not commutative for \(n \ge 2\).

The commutative ring \(\mathbb Z[\sqrt{2}] = \{a + b\sqrt{2} \ ; \ (a,b) \in \mathbb Z^2\}\) is not a field. However it has infinitely many units.

\(a + b\sqrt{2}\) is a unit if and only if \(a^2-2b^2 = \pm 1\)

For \(u = a + b\sqrt{2} \in \mathbb Z[\sqrt{2}]\) we denote \(\mathrm N(u) = a^2- 2b^2 \in \mathbb Z\). For any \(u,v \in \mathbb Z[\sqrt{2}]\) we have \(\mathrm N(uv) = \mathrm N(u) \mathrm N(v)\). Therefore for a unit \(u \in \mathbb Z[\sqrt{2}]\) with \(v\) as multiplicative inverse, we have \(\mathrm N(u) \mathrm N(v) = 1\) and \(\mathrm N(u) =a^2-2b^2 \in \{-1,1\}\).

The elements \((1+\sqrt{2})^n\) for \(n \in \mathbb N\) are unit elements

The proof is simple as for \(n \in \mathbb N\) \[
(1+\sqrt{2})^n (-1 + \sqrt{2})^n = \left((1+\sqrt{2})(-1 + \sqrt{2})\right)^n=1\]

One can prove (by induction on \(b\)) that the elements \((1+\sqrt{2})^n\) are the only units \(u \in \mathbb Z[\sqrt{2}]\) for \(u \gt 1\).

Analysis

A strictly increasing continuous function that is differentiable at no point of a null set

Leave a comment

We build in this article a strictly increasing continuous function \(f\) that is differentiable at no point of a null set \(E\). The null set \(E\) can be chosen arbitrarily. In particular it can have the cardinality of the continuum like the Cantor null set.

A set of strictly increasing continuous functions

For \(p \lt q\) two real numbers, consider the function \[
f_{p,q}(x)=(q-p) \left[\frac{\pi}{2} + \arctan{\left(\frac{2x-p-q}{q-p}\right)}\right]\] \(f_{p,q}\) is positive and its derivative is \[
f_{p,q}^\prime(x) = \frac{2}{1+\left(\frac{2x-p-q}{q-p}\right)^2}\] which is always strictly positive. Hence \(f_{p,q}\) is strictly increasing. We also have \[
\lim\limits_{x \to -\infty} f_{p,q}(x) = 0 \text{ and } \lim\limits_{x \to \infty} f_{p,q}(x) = \pi(q-p).\] One can notice that for \(x \in (p,q)\), \(f_{p,q}^\prime(x) \gt 1\). Therefore for \(x, y \in (p,q)\) distinct we have according to the mean value theorem \(\frac{f_{p,q}(y)-f_{p,q}(x)}{y-x} \ge 1\).

Covering \(E\) with an appropriate set of open intervals

As \(E\) is a null set, for each \(n \in \mathbb N\) one can find an open set \(O_n\) containing \(E\) and measuring less than \(2^{-n}\). \(O_n\) can be written as a countable union of disjoint open intervals as any open subset of the reals. Then \(I=\bigcup_{m \in \mathbb N} O_m\) is also a countable union of open intervals \(I_n\) with \(n \in \mathbb N\). The sum of the lengths of the \(I_n\) is less than \(1\). Continue reading A strictly increasing continuous function that is differentiable at no point of a null set →

Analysis

A monotonic function whose points of discontinuity form a dense set

Leave a comment

Consider a compact interval \([a,b] \subset \mathbb R\) with \(a \lt b\). Let’s build an increasing function \(f : [a,b] \to \mathbb R\) whose points of discontinuity is an arbitrary dense subset \(D = \{d_n \ ; \ n \in \mathbb N\}\) of \([a,b]\), for example \(D = \mathbb Q \cap [a,b]\).

Let \(\sum p_n\) be a convergent series of positive numbers whose sum is equal to \(p\) and define \(\displaystyle f(x) = \sum_{d_n \le x} p_n\).

\(f\) is strictly increasing

For \(a \le x \lt y \le b\) we have \[
f(y) – f(x) = \sum_{x \lt d_n \le y} p_n \gt 0\] as the \(p_n\) are positive and dense so it exists \(p_m \in (x, y]\).

\(f\) is right-continuous on \([a,b]\)

We pick-up \(x \in [a,b]\). For any \(\epsilon \gt 0\) is exists \(N \in \mathbb N\) such that \(0 \lt \sum_{n \gt N} p_n \lt \epsilon\). Let \(\delta > 0\) be so small that the interval \((x,x+\delta)\) doesn’t contain any point in the finite set \(\{p_1, \dots, p_N\}\). Then \[
0 \lt f(y) – f(x) \le \sum_{n \gt N} p_n \lt \epsilon,\] for any \(y \in (x,x+\delta)\) proving the right-continuity of \(f\) at \(x\). Continue reading A monotonic function whose points of discontinuity form a dense set →

Algebra

A normal extension of a normal extension may not be normal

Leave a comment

An algebraic field extension \(K \subset L\) is said to be normal if every irreducible polynomial, either has no root in \(L\) or splits into linear factors in \(L\).

One can prove that if \(L\) is a normal extension of \(K\) and if \(E\) is an intermediate extension (i.e., \(K \subset E \subset L\)), then \(L\) is a normal extension of \(E\).

However a normal extension of a normal extension may not be normal and the extensions \(\mathbb Q \subset \mathbb Q(\sqrt{2}) \subset \mathbb Q(\sqrt[4]{2})\) provide a counterexample. Let’s prove it.

As a short lemma, we prove that a quadratic extension \(k \subset K\) , i.e. an extension of degree two is normal. Suppose that \(P\) is an irreducible polynomial of \(k[x]\) with a root \(a \in K\). If \(a \in k\) then the degree of \(P\) is equal to \(1\) and we’re done. Otherwise \((1, a)\) is a basis of \(K\) over \(k\) and there exist \(\lambda, \mu \in k\) such that \(a^2 = \lambda a +\mu\). As \(a \notin k\), \(Q(x)= x^2 – \lambda x -\mu\) is the minimal polynomial of \(a\) over \(k\). As \(P\) is supposed to be irreducible, we get \(Q = P\). And we can conclude as \[
Q(x) = (x-a)(x- \lambda +a).\]

The entensions \(\mathbb Q \subset \mathbb Q(\sqrt{2})\) and \(\mathbb Q(\sqrt{2}) \subset \mathbb Q(\sqrt[4]{2})\) are quadratic, hence normal according to previous lemma and \(\sqrt[4]{2}\) is a root of the polynomial \(P(x)= x^4-2\) of \(\mathbb Q[x]\). According to Eisenstein’s criterion \(P\) is irreducible over \(\mathbb Q\). However \(\mathbb Q(\sqrt[4]{2}) \subset \mathbb R\) while the roots of \(P\) are \(\pm \sqrt[4]{2}, \pm i \sqrt[4]{2}\) and therefore not all real. We can conclude that \(\mathbb Q \subset \mathbb Q(\sqrt[4]{2})\) is not normal.

Algebra

The image of an ideal may not be an ideal

Leave a comment

If \(\phi : A \to B\) is a ring homomorphism then the image of a subring \(S \subset A\) is a subring \(\phi(A) \subset B\). Is the image of an ideal under a ring homomorphism also an ideal? The answer is negative. Let’s provide a simple counterexample.

Let’s take \(A=\mathbb Z\) the ring of the integers and for \(B\) the ring of the polynomials with integer coefficients \(\mathbb Z[x]\). The inclusion \(\phi : \mathbb Z \to \mathbb Z[x]\) is a ring homorphism. The subset \(2 \mathbb Z \subset \mathbb Z\) of even integers is an ideal. However \(2 \mathbb Z\) is not an ideal of \(\mathbb Z[x]\) as for example \(2x \notin 2\mathbb Z\).

Analysis

A function whose Maclaurin series converges only at zero

Leave a comment

Let’s describe a real function \(f\) whose Maclaurin series converges only at zero. For \(n \ge 0\) we denote \(f_n(x)= e^{-n} \cos n^2x\) and \[
f(x) = \sum_{n=0}^\infty f_n(x)=\sum_{n=0}^\infty e^{-n} \cos n^2 x.\] For \(k \ge 0\), the \(k\)th-derivative of \(f_n\) is \[
f_n^{(k)}(x) = e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right)\] and \[
\left\vert f_n^{(k)}(x) \right\vert \le e^{-n} n^{2k}\] for all \(x \in \mathbb R\). Therefore \(\displaystyle \sum_{n=0}^\infty f_n^{(k)}(x)\) is normally convergent and \(f\) is an indefinitely differentiable function with \[
f^{(k)}(x) = \sum_{n=0}^\infty e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right).\] Its Maclaurin series has only terms of even degree and the absolute value of the term of degree \(2k\) is \[
\left(\sum_{n=0}^\infty e^{-n} n^{4k}\right)\frac{x^{2k}}{(2k)!} > e^{-2k} (2k)^{4k}\frac{x^{2k}}{(2k)!} > \left(\frac{2kx}{e}\right)^{2k}.\] The right hand side of this inequality is greater than \(1\) for \(k \ge \frac{e}{2x}\). This means that for any nonzero \(x\) the Maclaurin series for \(f\) diverges.

Algebra

A group that is not a semi-direct product

1 Comment

Given a group \(G\) with identity element \(e\), a subgroup \(H\), and a normal subgroup \(N \trianglelefteq G\); then we say that \(G\) is the semi-direct product of \(N\) and \(H\) (written \(G=N \rtimes H\)) if \(G\) is the product of subgroups, \(G = NH\) where the subgroups have trivial intersection \(N \cap H= \{e\}\).

Semi-direct products of groups provide examples of non abelian groups. For example the dihedral group \(D_{2n}\) with \(2n\) elements is isomorphic to a semidirect product of the cyclic groups \(\mathbb Z_n\) and \(\mathbb Z_2\). \(D_{2n}\) is the group of isometries preserving a regular polygon \(X\) with \(n\) edges.

Let’see that the converse is not true and present a group that is not a semi-direct product.

The Hamilton’s quaternions group is not a semi-direct product

The Hamilton’s quaternions group \(\mathbb H_8\) is the group consisting of the symbols \(\pm 1, \pm i, \pm j, \pm k\) where\[
-1 = i^2 =j^2 = k^2 \text{ and } ij = k = -ji,jk = i = -kj, ki = j = -ik.\] One can prove that \(\mathbb H_8\) endowed with the product operation above is indeed a group having \(8\) elements where \(1\) is the identity element.

\(\mathbb H_8\) is not abelian as \(ij = k \neq -k = ji\).

Let’s prove that \(\mathbb H_8\) is not the semi-direct product of two subgroups. If that was the case, there would exist a normal subgroup \(N\) and a subgroup \(H\) such that \(G=N \rtimes H\).

  • If \(\vert N \vert = 4\) then \(H = \{1,h\}\) where \(h\) is an element of order \(2\) in \(\mathbb H_8\). Therefore \(h=-1\) which is the only element of order \(2\). But \(-1 \in N\) as \(-1\) is the square of all elements in \(\mathbb H_8 \setminus \{\pm 1\}\). We get the contradiction \(N \cap H \neq \{1\}\).
  • If \(\vert N \vert = 2\) then \(\vert H \vert = 4\) and \(H\) is also normal in \(G\). Noting \(N=\{1,n\}\) we have for \(h \in H\) \(h^{-1}nh=n\) and therefore \(nh=hn\). This proves that the product \(G=NH\) is direct. Also \(N\) is abelian as a cyclic group of order \(2\). \(H\) is also cyclic as all groups of order \(p^2\) with \(p\) prime are abelian. Finally \(G\) would be abelian, again a contradiction.

We can conclude that \(G\) is not a semi-direct product.

Analysis

Painter’s paradox

Leave a comment

Can you paint a surface with infinite area with a finite quantity of paint? For sure… let’s do it!

Consider the 3D surface given in cylindrical coordinates as \[
S(\rho,\varphi):\begin{cases}
x &= \rho \cos \varphi\\
y &= \rho \sin \varphi\\
z &= \frac{1}{\rho}\end{cases}\] for \((\rho,\varphi) \in [1,\infty) \times [0, 2 \pi)\). The surface is named Gabriel’s horn.

Volume of Gabriel’s horn

The volume of Gabriel’s horn is \[
V = \pi \int_1^\infty \left( \frac{1}{\rho^2} \right) \ d\rho = \pi\] which is finite.

Area of Gabriel’s horn

The area of Gabriel’s horn for \((\rho,\varphi) \in [1,a) \times [0, 2 \pi)\) with \(a > 1\) is: \[
A = 2 \pi \int_1^a \frac{1}{\rho} \sqrt{1+\left( -\frac{1}{\rho^2} \right)^2} \ d\rho \ge 2 \pi \int_1^a \frac{d \rho}{\rho} = 2 \pi \log a.\] As the right hand side of inequality above diverges to \(\infty\) as \(a \to \infty\), we can conclude that the area of Gabriel’s horn is infinite.

Conclusion

Gabriel’s horn could be filled with a finite quantity of paint… therefore painting a surface with infinite area. Unfortunately the thickness of the paint coat is converging to \(0\) as \(z\) goes to \(\infty\), leading to a paint which won’t be too visible!

Algebra

A normal subgroup that is not a characteristic

Leave a comment

Let’s \(G\) be a group. A characteristic subgroup is a subgroup \(H \subseteq G\) that is mapped to itself by every automorphism of \(G\).

An inner automorphism is an automorphism \(\varphi \in \mathrm{Aut}(G)\) defined by a formula \(\varphi : x \mapsto a^{-1}xa\) where \(a\) is an element of \(G\). An automorphism of a group which is not inner is called an outer automorphism. And a subgroup \(H \subseteq G\) that is mapped to itself by every inner automorphism of \(G\) is called a normal subgroup.

Obviously a characteristic subgroup is a normal subgroup. The converse is not true as we’ll see below.

Example of a direct product

Let \(K\) be a nontrivial group. Then consider the group \(G = K \times K\). The subgroups \(K_1=\{e\} \times K\) and \(K_2=K \times \{e\} \) are both normal in \(G\) as for \((e, k) \in K_1\) and \((a,b) \in G\) we have
\[(a,b)^{-1} (e,x) (a,b) = (a^{-1},b^{-1}) (e,x) (a,b) = (e,b^{-1}xb) \in K_1\] and \(b^{-1}K_1 b = K_1\). Similar relations hold for \(K_2\). As \(K\) is supposed to be nontrivial, we have \(K_1 \neq K_2\).

The exchange automorphism \(\psi : (x,y) \mapsto (y,x)\) exchanges the subgroup \(K_1\) and \(K_2\). Thus, neither \(K_1\) nor \(K_2\) is invariant under all the automorphisms, so neither is characteristic. Therefore, \(K_1\) and \(K_2\) are both normal subgroups of \(G\) that are not characteristic.

When \(K = \mathbb Z_2\) is the cyclic group of order two, \(G = \mathbb Z_2 \times \mathbb Z_2\) is the Klein four-group. In particular, this gives a counterexample where the ambient group is an abelian group.

Example on the additive group \(\mathbb Q\)

Consider the additive group \((\mathbb Q,+)\) of rational numbers. The map \(\varphi : x \mapsto x/2\) is an automorphism. As \((\mathbb Q,+)\) is abelian, all subgroups are normal. However, the subgroup \(\mathbb Z\) is not sent into itself by \(\varphi\) as \(\varphi(1) = 1/ 2 \notin \mathbb Z\). Hence \(\mathbb Z\) is not a characteristic subgroup.

Mathematical exceptions to the rules or intuition