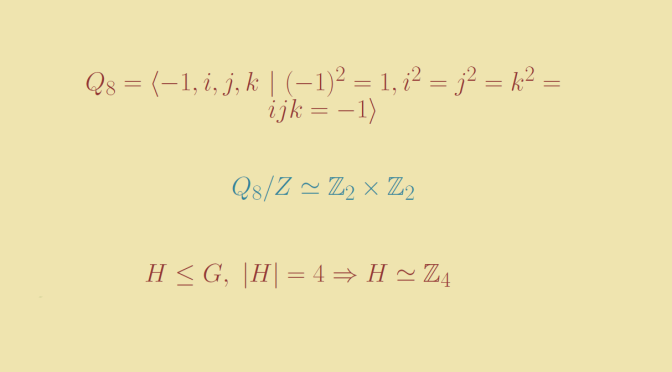Given a normal subgroup \(H\) of a finite group \(G\), is \(G/H\) always isomorphic to a subgroup \(K \le G\)?
The case of an abelian group
According to the fundamental theorem of finite abelian groups, every finite abelian group \(G\) can be expressed as the direct sum of cyclic subgroups of prime-power order: \[G \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i}}\] where \(p_1, \dots , p_u\) are primes and \(\alpha_1, \dots , \alpha_u\) non zero integers.
If \(H \le G\) we have \[H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\beta_i}}\] with \(0 \le \beta_1 \le \alpha_1, \dots, 0 \le \beta_u \le \alpha_u\). Then \[G/H \simeq \bigoplus_{i=1}^u \mathbb{Z}_{p_i^{\alpha_i-\beta_i}}\] which is a subgroup of \(G\).
If \(G\) is not abelian, then \(G/H\) might not be isomorphic to a subgroup of \(G\).
The case of the quaternion group \(Q_8\)
Consider the quaternion group \[Q_8 =\langle -1,i,j,k \ | \ (-1)^2=1,i^2=j^2=k^2=ijk=-1\rangle\]
The center of \(Q_8\) is \(Z=\{-1,1\}\) as we have the relations:\[\left\{
\begin{array}{ccc}
ij=k & , & ji=-k \\
jk=i & , & kj=-i \\
ki=j & , & ij=-i \\
\end{array}
\right.\]
\(Q_8/Z\) has order four and all elements of \(Q_8/Z\) have order two as for \(x \in Q_8\), \(x^2 \in \{-1,1\}\). On the other hand the order four subgroups of \(Q_8\) are \(\langle i \rangle, \langle j \rangle, \langle k \rangle\) which are cyclic and isomorphic to \(\mathbb Z_4\).
Finally \(Q_8/Z\) cannot be isomorphic to a subgroup of \(G\).